Vyhledávání úloh podle oboru

Každá kapalina má svou specifickou viskozitu. Pokuste se doma vyrobit průtokový viskozimetr a změřit relativní viskozitu několika vhodných tekutin (alespoň tří) vůči vodě. Vaše výsledky porovnejte s údaji vyhledanými na internetu.

Kužel obrácený podstavou vzhůru může držet ve vzduchu na stříkajícím proudu vody, který vychází ze země s konstantním hmotnostním průtokem a počáteční rychlostí $v_{0}$. V jaké výšce nad zemí se bude kužel v rovnováze vznášet?

Bonus: Vyšetřete stabilitu kužele v této poloze.

Máme malou kulatou bublinku plynu v kapalině, která teče nějakou rychlostí vodorovným potrubím. Jak se změní její rozměry, když se dostane do místa, kde je potrubí zúžené? K čemu se to dá využít, nebo naopak kde to dělá problémy? Uvažujte laminární proudění.

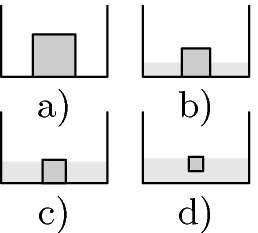
Na dně prázdného bazénu s dnem plochy $S$ leží ledová kostka (z vody) o hraně délky $a$. Kostka se rozpouští ze všech stran stejnoměrně tak, že si je stále podobná. Jaká její část se rozpustí, než začne plovat?

O kolik se zvýší rychlost čepování čaje $v_{0}$, pokud je do várnice právě doléván? Průměr várnice je $D$, průměr proudu dolévaného čaje je $d$ právě při dopadu na hladinu. Čaj naléváme z výšky $h$ nad hladinou, která je ve výšce $H$ nad středem otvoru. Průměr otvoru, jímž čaj vytéká, je mnohem menší než $D$. Zanedbejte veškeré tření.

Odhadněte, kolik energie by bylo potřeba na odpaření všech pozemských oceánů.

Určete, jak závisí rychlost vypařování vody na povrchu, který tato kapalina zaujímá. Experiment proveďte alespoň pro pět různých vhodných nádob. Zamyslete se nad dalšími faktory, které mohou rychlost vypařování vody ovlivnit. Upozorňujeme, že experiment je velmi vhodné nechat probíhat po delší dobu (několik dní), proto ideálně začněte o hodně dřív než pár hodin před uzávěrkou.

Vzpomeňte si na velké povodně z roku 2002. Odhadněte, kolik vody pojme pražské metro při povodních. Důležité rozměry jako velikosti souprav, počet stanic, celkovou délku tubusů metra a další si najděte na internetu.

V U-trubici je rtuť se vzduchovou bublinou výšky $h_{0}$ v jednom rameni, jak můžete vidět na obrázku. Co se stane, pokud se okolní atmosféra změní následujícími způsoby? Předpokládejte, že rtuť při změně teploty nemění objem (hustotu), stejně tak i sklo, ze kterého je U-trubice, a vzduch se chová jako ideální plyn. Původní stav okolní atmosféry je popsán teplotou $T_{0}=300K$, tlakem $p_{a}=10\cdot 10^{5}Pa$ a složením je vzduch. Předpokládejte, že celý systém je stále v termodynamické rovnováze, rovněž bublinu považujte za válec.

• Okolní teplota se zvýší na dvojnásobek a přitom budou ramena U-trubice volná.
• Okolní teplota se zvýší na dvojnásobek, ale před touto změnou pevně uzavřeme oba konce U-trubice.
• Okolní teplota se zvýší na dvojnásobek, ale před zahřátím pevně uzavřeme pouze jeden konec U-trubice. Pro všechny body zadání určete výsledné rozměry bubliny ve rtuti a výškový rozdíl mezi hladinami v obou částech U-trubice.

Bonus: Započtěte lineární teplotní roztažnost rtuti.

Jaká část povrchu ledové kry tvaru koule trčí nad hladinu? Hustota ledu je $917\;\mathrm{kg/m^3}$, hustota mořské vody $1025\;\mathrm{kg/m^3}$.