Vyhledávání úloh podle oboru

Děla na bitevních lodích se nabíjejí následujícím způsobem: do hlavně se dá střela o hmotnosti $M$ a za ní určitý počet balíku s výbušninou (objem jednoho balíku je $V_{0})$, podle toho jak daleko chceme střílet. Kolikrát se zvětší dostřel takového děla, když nabijeme dvojnásobné množství výbušniny? Výbuch si představujte tak, že najednou se místo výbušniny objeví dvouatomový plyn o teplotě $T_{0}$ a tlaku $p_{0}$. Ráže děla je deset palců. Odpor vzduchu zanedbejte.

Ve Švýcarsku plánují vybudování celostátního „metra“. Vlaky mají jezdit na magnetickém polštáři tunelem, ze kterého je částečně vyčerpaný vzduch, a dosahovat rychlosti kolem $500\, \jd{km.h^{-1}}$. Tunel však nelze dokonale utěsnit. Předpokládejme, že chceme udržet tlak na hodnotě $0,05 p_{a}$, ale bez neustálého odčerpávání by za 1 den vzrostl na $0,5 p_{a}$. Spočtěte výkon, jaký je nutný na odčerpávání vzduchu ze $100 \jd{km}$ tohoto tunelu, je-li jeho průměr $5 \jd{m}$, účinnost odčerpávání oproti ideálně pracujícímu stroji $10\%$ a teplota $6 ^{\circ}C$. S čím lze takový výkon porovnat?

Ve velké nádobě s vodou je částečně ponořena dnem vzhůru válcová sklenice. Hladina vody v nádobě i ve sklenici je stejná a je vzdálena $l=10\jd{ cm}$ ode dna sklenice. Teplota vzduchu je $t_{0}=20\jd{^{\circ}C}$ a atmosférický tlak je $p_{0}=100\jd{ kPa}$. O jakou výšku $h$ stoupne hladina vody ve sklenici, jestliže se teplota sníží o $\Delta t=10\jd{^{\circ}C}$ a tlak stoupne o $\Delta p=2,0\jd{ kPa}$?

Za jak dlouho se vypaří voda ze sklenice o výšce $h=10\,\jd{cm}$ za normálních podmínek? Předpokládejte, že vlhkost vzduchu těsně nad hladinou je neustále $99\%$

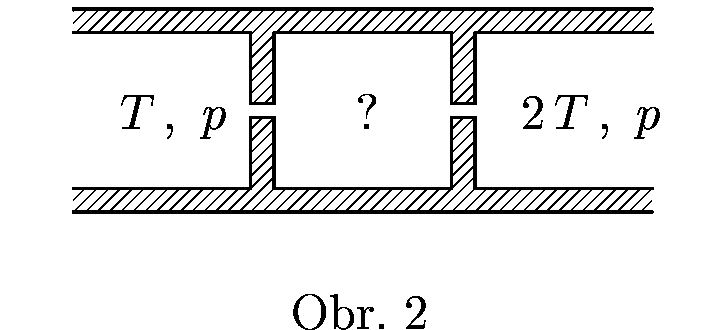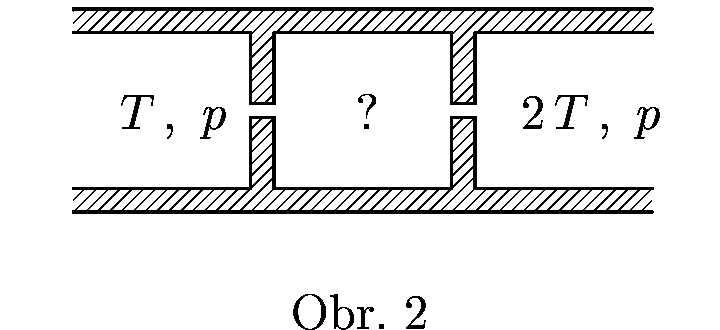
Představme si podle obrázku nádobu s ideálním plynem rozdělenou dvěma přepážkami na tři části. Napravo se udržuje teplota $T$ a tlak $p$, nalevo $2 \,\jd{T}$ a $p$. Určete, jaká teplota a tlak je v prostřední části, víte-li, že celý systém je v dynamické rovnováze.

Uzavřená nádoba obsahující ideální plyn se pohybuje rychlostí $v$. Nádoba se náhle zastaví a veškerá kinetická energie plynu se změní v teplo. Zanedbejte teplo předané stěnám a spočtěte, o kolik se zvětší druhá mocnina střední kvadratické rychlosti molekul plynu, je-li plyn

• jednoatomový
• dvouatomový.

Zdůvodněte rozdílné výsledky v jednotlivých případech.

Když vezmeme list papíru a pustíme jej ve vodorovné poloze, začne pomalu padat. Pokud jej přehneme na polovinu, bude padat rychleji – toť známý fakt. Vaším úkolem je pomocí tohoto jevu zjistit, podle jakého vztahu se mění odporová síla vzduchu působící na papír (závisí na rychlosti lineárně či kvadraticky?). Pokuste se určit potřebné konstanty.

Vzduch v horkovzdušném balónu je zahříván konstantním příkonem, aby se vyrovnaly tepelné ztráty a balón letěl stále ve stejné výšce. Průměrná teplota vzduchu v balónu je $t=57\;\mathrm{°C}$, teplota okolního vzduchu je $t_{0}=17\;\mathrm{°C}$. Tlak vzduchu v balónu je roven okolnímu tlaku. Pokud zvýšíme příkon hořáku tak, aby teplota v balónu vzrostla o $Δt=0,1\;\mathrm{°C}$, o kolik se změní výška letu balónu?

Tenkou ploskodutou čočku s poloměrem křivosti lámavé plochy $R$ postupně ponořujeme do vody (viz obrázek). Nalezněte závislost optické mohutnosti takovéto soustavy na hloubce ponoření čočky. Znáte index lomu skla, vody a vzduchu při atmosférickém tlaku. Závislost indexu lomu vzduchu na tlaku je lineární.

Spočtěte co nejpřesněji, jakou hmotnost má zemská atmosféra.