Vyhledávání úloh podle oboru

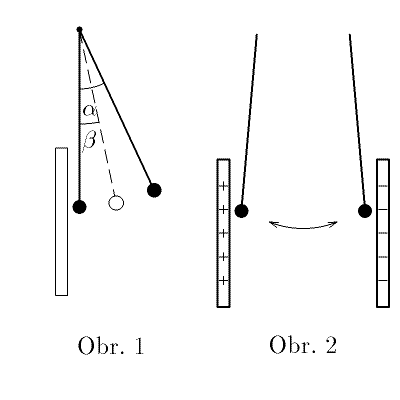
Malá kovová kulička o hmotnosti $m=3,0\,\jd{g}$ je zavěšena na tenkém hedvábném vlákně délky $l=30\;\mathrm{cm}$ tak, aby se dotýkala svislé kovové desky. Kuličku vychýlíme o úhel $α$ a uvolníme. Po odrazu od desky se kulička vychýlí o úhel $β<α$ (obr. 1).

Při druhém pokusu umístíme do vzdálenosti $d=5,0\;\mathrm{cm}$ od první desky druhou stejně velkou. Závěs kuličky prodloužíme, aby byl mnohem delší než vzdálenost desek. Připojíme-li desky ke zdroji vysokého napětí $U=2,00\cdot 10^{4}$ V a závěs vychýlíme, kulička se rozkmitá a naráží střídavě na levou a pravou desku (obr. 2). Perioda nárazů se brzy ustálí na hodnotě $T=0,45\;\mathrm{s}$.

Jak se mění při druhém pokusu rychlost kuličky mezi dvěma nárazy na desky? Jaký náboj nese kulička během letu mezi deskami?

Mějme rovnoměrně nabitou kovovou kulovou slupku s poloměrem $R$ a s celkovým nábojem $Q$. Rozřízněme ji na dvě části rovinou, která je od středu koule vzdálena $d<R$. Úkolem je spočíst sílu, jakou se obě části budou odpuzovat, dokud jsou velmi blízko sebe.

Lidské srdce napumpuje za minutu $q=5\,\jd{l}$ krve při tlaku $p=100\;\mathrm{mm}Hg$. Kolik dní by byla schopna konat stejnou práci standardní autobaterie s účinností $\eta=50%?$ ($Q=48\,\jd{Ah}$, $U=12\,\jd{V}$).

Tři koule jsou spojeny stejnými gumičkami tak, že tvoří rovnostranný trojúhelník. Soustava leží na hladkém vodorovném stole. Jaké náboje je třeba na koule přivést, aby se plocha trojúhelníka zdvojnásobila? Tuhost gumiček je $k$, počáteční délka je $l$.

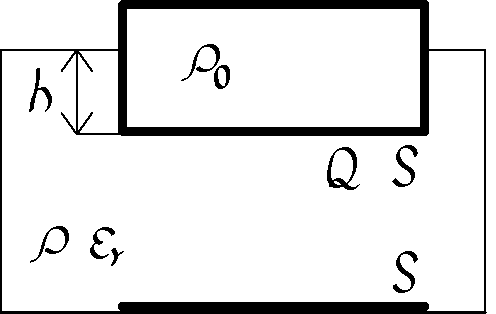
Velká nádoba je naplněna tekutým dielektrikem hustoty $ρ$ a relativní permitivity $ε_{r}$. Na dně nádoby je tenká kovová deska o ploše $S$. Nad ní plave vodivý hranol hustoty $ρ_{0}<ρ$, jehož podstava má obsah $S$. Na hranol přivedeme elektrický náboj $Q$ (viz obrázek). Jak ovlivní elektrické pole hloubku ponoru hranolu, víte-li, že

• deska na dně je uzemněna
• deska není uzemněna

Zaveďte takové zjednodušující předpoklady, abyste byli schopni úlohu řešit, a pokuste se odhadnout chybu, kterou vaše zjednodušení do výsledku vnesou.

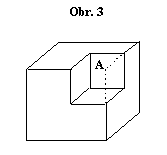
Představme si krychli s rovnoměrně rozloženým nábojem o hustotě $r$ v celém jejím objemu. Ve vrcholu $A$ jsme naměřili intenzitu elektrického pole $\textbf{E}$. Jakou intenzitu naměříme v bodě $A$, jestliže vyřízneme z krychle krychličku o poloviční délce hrany, jak je znázorněno na obr. 3?

Kondenzátor ze dvou desek plochy $S$ vzdálených o $l_{1}$ nabijeme baterií na napětí $U_{b}$. Jakou práci musíme vykonat k oddálení desek na vzdálenost $l_{2}$, když jsme před tím baterii

• odpojili,
• neodpojili.

Jestliže se práce v případě a) a b) liší, vysvětlete, jaké „tajemné síly“ tento rozdíl způsobují. Rozměry desek jsou mnohem větší než vzdálenosti $l_{1}$, $l_{2}$.

Nabitá částice vstupuje do prostředí, ve kterém na ni působí odporová síla. Směr této síly je opačný, než směr rychlosti částice, a její velikost je rychlosti přímo úměrná. Než se částice zastaví, urazí v prostředí dráhu $l_{1}=10\;\mathrm{cm}$. Je-li v prostředí navíc homogenní magnetické pole kolmé na směr rychlosti částice, pak se částice zastaví ve vzdálenosti $l_{2}=6\;\mathrm{cm}$ od místa, kde do prostředí vstoupila. V jaké vzdálenosti $l_{3}$ od místa vstupu do prostředí se částice zastaví, když bude magnetické pole dvakrát menší?

Tři stejné ploché rovinné desky A, B a C, každá o obsahu $S$, jsou umístěny rovnoběžně ve vzdálenostech $d_{1}$ a $d_{2}$ (viz obrázek). Jsou izolovány, na deskách B a C je náboj +$q$ a −$q$, deska A není nabita. Desky A a C spojíme přes odpor $R$ stisknutím spínače K. Najděte množství tepla uvolněného v odporu do vyrovnání potenciálů.

Kondenzátor z dvou desek plochy $S$ vzdálených $l_{1}$ nabijeme baterií o napětí $U_{B}$. Jaku práci musíme vykonat k oddálení desek na vzdálenost $l_{2}$, když jsme přetím baterii

• odpojili
• neodpojili

Jestliže se práce v případě a) a b) liší, vysvětlete, jaké „tajemné síly“ tento rozdíl způsobují. Rozměry desek jsou mnohem větší než vzdálenosti $l_{1}$ a $l_{2}$.