Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika plynů
2. Série 12. Ročníku - P. ve výtahu
U každého výtahu v mrakodrapu je jisté riziko, že se zpřetrhají všechna lana, na kterých visí. Abychom předešli případnému úrazu, můžeme výtah vylepšit: Spodní část výtahové šachty utěsníme tak, abychom zamezili úniku vzduchu. Také okolo kabiny výtahu dáme těsnění. Výtah, který se utrhne v horním patře mrakodrapu se zabrzdí o vzduchový polštář, který si pod sebou stlačí. Předpokládejte, že kabina vážící $1000\,\jd{ kg}$ se utrhla $87\,\jd{ m}$ vysoko a vzduchotěsná část výtahové šachty začíná $15\,\jd{ m}$ nad zemí. Jak vysoko nad zemí se kabina nakonec zastaví? Jak velké síly působí po dobu pádu na cestující? V případě výpočtu síly se spokojíme i s kvalifikovaným odhadem, přesný výpočet bude po zásluze odměněn.
1. Série 12. Ročníku - 4. roztržitý výletník
Roztržitý výletník zaparkoval své auto na kopci se sklonem $\alpha=10^{\circ}$ a zapomněl jej zabrzdit. Jaké maximální rychlosti auto dosáhne? Parametry auta jsou: hmotnost $m=1200\;\mathrm{kg}$, výkon $P=55\,\jd{kW}$, maximální rychlost na rovné silnici $v_{max}=140\;\mathrm{km} \cdot \mathrm{h}^{-1}$. Předpokládejte že, odpor automobilu je úměrný druhé mocnině rychlosti.
5. Série 11. Ročníku - 1. dvojpíst
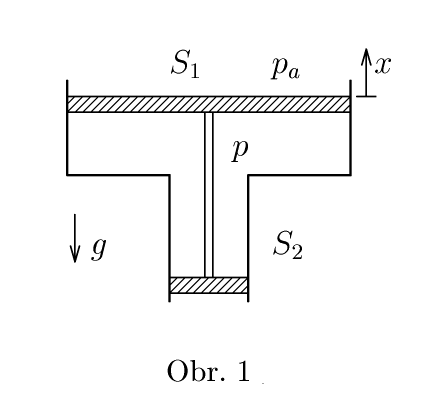
Píst
Na obrázku obr. 1 vidíte dva spojené písty o ploše $S_{1}$ a $S_{2}$ a celkové hmotnosti $m$ zasunuté do pouzdra, které je na obou stranách otevřené. Celé zařízení je v rovnováze a je umístěno v tíhovém poli $g$. Vně pístů je atmosférický tlak $p_{a}$, uvnitř je $1\,\jd{kmol}$ ideálního plynu o tlaku $p$. O kolik stupňů Celsia musíme plyn mezi písty ohřát, aby se písty posunuly o $x$ směrem vzhůru?
4. Série 11. Ročníku - E. křídový prach
Změřte poloměr zrnka křídového prachu.
Pomůcka: Pro velmi jemný prach můžeme měřit dobu pádu prachu na zem a za pomoci Stokesova vzorce pro odpor prostředí můžeme poloměr dopočítat.
4. Série 11. Ročníku - P. levitující kapalina
Jistě jste si už někdy všimli, že když vytahujeme skleničku z umyvadla dnem vzhůru, zůstává v ní voda až do té chvíle, kdy její okraj vytáhneme nad hladinu. Pak všechna vyteče. Vysvětlete proč. Uvědomte si, že na povrch kapaliny ve skleničce obrácené dnem vzhůru působí tlak vzduchu, který dokáže vytlačit až deset metrů vodního sloupce!
2. Série 11. Ročníku - 4. kapka deště
Jeden náš řešitel, který se vracel ze soustředění za deštivého počasí vlakem domů si všiml, že kapky na skle vytvářejí přímé stopy. Změřil, že jsou od svislého směru odkloněny o úhel $α=35^{o}$. Určete jakou rychlostí jel vlak, mají-li kapky poloměr $r=2\;\mathrm{mm}$.
6. Série 10. Ročníku - 4. lanovka
Na Šumavě se v současnosti buduje zajímavé zařízení na přepravu dřeva. Protože se do močálu normální traktor nedostane, pokoušejí se lesníci použít pro přepravu dřeva vzducholodě. Vzducholoď bude mít nosnost $5000\, \jd{kg}$ a bude upevněna ke dvěma stanovištím vzdálených od sebe $3\, \jd{km}$. Vzducholoď nemá žádný pohon a je tahána mezi kotvícími stanovišti. Jednu cestu absolvuje naložená dřeva a druhou jede prázdná, občas nesa vaky s vodou. Jakou maximální silou bude vzducholoď působit na upevňovací lana, bude-li prázdná a nesmí-li její výška nad terénem přesáhnout $300\, \jd{m}$ (aby nenarušila vzdušný prostor) na celé tříkilometrové trase?
4. Série 10. Ročníku - P. fotbalistický problém
Fotbalista vykopne míč a udělí mu kromě posuvné rychlosti i rotaci okolo svislé osy. Na kterou stranu od původního směru se míč začne odchylovat v závislosti na smyslu rotace a proč? Míč považujte za ideální kouli, odpor vzduchu nezanedbávejte.
4. Série 9. Ročníku - 3. stvoření hvězd
Podle jedné z teorií vznikají hvězdy z oblaku mezihvězdné látky (kosmického prachu) smršťováním pod vlivem gravitačních sil. Určete dobu, za jakou se může zformovat hvězda z obrovského kulového oblaku kosmického prachu o hustotě $ρ=2\cdot 10^{–17}\;\textrm{kg}\cdot \textrm{m}^{–3}$. Můžete předpokládat, že se během smršťování částečky hmoty nepředbíhají a na začátku smršťování měly nulové rychlosti (oblak nijak nerotoval, nebyly v něm víry apod.). Zanedbejte také rozměry vzniknuvší hvězdy vůči počáteční velikosti oblaku.
2. Série 9. Ročníku - P. Lomonosův průvan
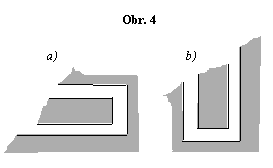
Velký přírodovědec M. V. Lomonosov studoval ve své světově proslulé práci „O volném pohybu vzduchu v dolech“ závislost směru proudění vzduchu na ročním období. Po dlouhém a strastiplném bádání dospěl k závěru, že teplota vzduchu je v dole stále stejná po celý rok. (V jeho době byly doly ještě poměrně mělké.) Určete, jakými směry bude vzduch proudit v létě a v zimě v dolech umístěných podle obr. 4.