Vyhledávání úloh podle oboru

Jak známo, vlaky nemají diferenciál, tedy při průjezdu zatáčkou se obě kola musí otáčet stejnou úhlovou rychlostí. Předpokládejte nyní, že kola mají válcový tvar. Proto při jízdě zatáčkou pojede jedno kolo po delší trajektorii než druhé. Osička bude namáhána na krut a v jistý okamžik již třecí síla mezi kolem a kolejnicí nebude dostatečně velká a dojde k prokluzu jednoho z kol, čímž napětí v osičce klesne na nulu. Určete vzdálenost mezi jednotlivými prokluzy v závislosti na poloměru zatáčky $R_{z}$. Kolo má poloměr $R$, osa má poloměr $r$, délka osy je $L$, modul pružnosti materiálu osy ve smyku je $G$ (ocel), vagon s $N$ koly má hmotnost $M$ a koeficient statického tření mezi kolem a kolejnicí je $f$. Nakonec můžete dosadit realistické hodnoty.

Nápověda: Pro zkrut $φ$ válce o poloměru $R$, délce $l$ a modulu pružnosti ve smyku $G$, na který působíme momentem $M$, platí:

$$\varphi=\frac{2Ml}{G \pi R^4}$$

Mějme houpačku zavěšenou na dvou svislých lanech délky $l=1,5\;\mathrm{m}$ na vodorovné tyči o poloměru $r=4\;\mathrm{cm}$. Dítěti sedícímu na houpačce udělíme v dolní úvrati takovou rychlost $v_{0}$, aby dítě vykonalo celou otočku kolem horizontální tyče a lana byla během namotávání stále napnutá. Zároveň chceme, aby počáteční rychlost byla nejmenší možná. Určete rozdíl úhlové rychlosti $ω_{1}$ houpačky s dítětem po návratu do dolní úvrati a počáteční úhlové rychlosti $ω_{0}$.

Nápověda: Pro výpočet odstředivého zrychlení můžete uvažovat, že se dítě pohybuje lokálně po kružnici.

Chudák hladový kojot chce ulovit proradného ptáka Uličníka a přichystal na něj následující past: na pevné lano přiváže 500tunovou kovadlinu, přehodí ji přes větev tak, aby visela nad silnicí, a bude čekat. Kolikrát musí lano kolem větve obtočit, jestliže chce kovadlinu udržet ve vzduchu pouze vlastní vahou? Předpokládejte, že hmotnost lana je vůči hmotnosti kojota zanedbatelná.

Máme nakloněnou rovinu, na které postrčíme míček, aby se začal kutálet bez prokluzování směrem nahoru po nakloněné rovině. Změřte závislost rychlosti míčku na čase a určete závislost ztráty energie na čase. Nakloněná rovina nechť svírá úhel s vodorovnou rovinou úhel $α=10°$. Nezapomeňte popsat parametry vašeho míčku.

Jak by musel být minimálně dlouhý ocelový drát ve stočeném stavu, aby se při volném zavěšení za jeho jeden konec přetrhl? Používáme ocelový drát o hustotě $ρ=7900\;\mathrm{kg}\cdot \mathrm{m}^{-3}$, průměru $D=1\;\mathrm{mm}$ a mezi pevnosti $σ_{max}=400\; \jd{MPa}$. Uvažujte, že jsme v homogenním tíhovém poli o intenzitě $g=9.81\;\mathrm{m}\cdot \mathrm{s}^{-2}$.

Bonus: Uvažujte teď nejdelší drát, který se ještě nepřetrhne. O kolik procent se protáhne po zavěšení? Youngův modul pružnosti v tahu použité oceli je $E=200\;\jd{GPa}$.

Mějme hráče baseballu, který drží v rukou baseballovou pálku délky $L$ a hmotnosti $m$ a chystá se na odpal míčku. Jako vhodné přiblížení se držme toho, že hráč může otáčet pálkou jen okolo fixované osy, která je kolmá na osu pálky a prochází na jejím konci rukama odpalujícího hráče. Pálkou otáčí úhlovou rychlostí $ω$. V jaké vzdálenosti $l$ od konce pálky má hráč odpálit míček, aby nárazová síla na hráčovy ruce byla co nejmenší? Pálka je tenká homogenní tyč.

Když pustíte nafukovací balónek z výšky, po chvíli bude padat s přibližně konstantní rychlostí. Změřte, jak závisí tato rychlost na velikosti balónku a na hmotnosti závaží, které pod něj zavěsíte.

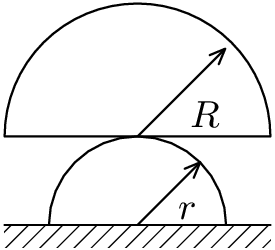
Mějme dva půlválce ležící na sobě jako na obrázku. Spodní má poloměr $r$ a horní poloměr $R$. Pro jaký poloměr $R$ s pevným $r$ je soustava stabilní?

Bonus: V případech, kdy je soustava stabilní (pokud vychýlíme vrchní válec z rovnovážné polohy, tak začne provádět malé kmity), s jakou periodou bude kmitat?

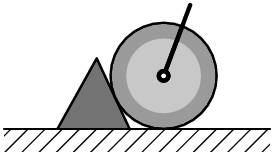
Může zašpalkované letadlo pustit motory na zemi na plný tah a zůstat na místě? Pokuste se o obecné vyjádření uvažující různé materiály kola, špalku i podlahy. Změní se to, bude-li špalek vysoký akorát na dotek kola?

Jaký je poměr objemu Země ku objemu Měsíce? Vypočítejte jej pouze ze znalosti, že poměr jejich hmotností je přibližně 81 a že intenzita gravitačního pole je na povrchu Země přibližně šestkrát vyšší než na povrchu Měsíce.