Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
astrofyzika
4. Série 10. Ročníku - 1. sever
Je to už dávno, co jsme my, organizátoři, chodili na své základní školy. Nicméně si všichni dobře pamatujeme, že jsme se učili, jak pomocí ručičkových hodinek a polohy Slunce na obloze přibližně stanovit sever. Po vás bychom chtěli, abyste nám vysvětlili, jak to funguje, proč to funguje a s jakou přesností (přibližně).
4. Série 10. Ročníku - S. Slunce a meteoroidy
Ověřte hypotézu, že zdrojem energie Slunce jsou meteoroidy dopadající na jeho povrch. Určete, kolik meteoroidů (jejich hmotnost) by muselo dopadnout na Slunce za 1 rok, aby se energeticky pokryl zářivý výkon Slunce $L=3,83\cdot 10^{26}\, \jd{W}$. Předpokládejte, že se vyzáří veškerá kinetická energie meteoroidů (ve skutečnosti se část této energie spotřebuje na ohřev Slunce a na změnu celkové potenciální energie Slunce). Poloměr Slunce je $R=6,96\cdot 10^{8}\, \jd{m}$, hmotnost $1,99\cdot 10^{30}\, \jd{kg}$. Určete, o kolik by se za rok změnila velká poloosa a doba oběhu Země díky nárůstu hmotnosti Slunce. Předpokládejte, že se hmotnost Slunce mění skokově a že před touto změnou obíhala Země kolem Slunce po kružnici o poloměru $a=1\;\mathrm{AU}=1,496\cdot 10^{11}\, \jd{m}$ s dobou oběhu $T = 1\, \jd{rok}$. Při výpočtu použijte přibližný vztah $(1 + x)^{k}=1+kx$, který platí pro $k$ reálné. Dnes je známa astronomická jednotka s přesností na 2 metry. Bylo by možné tuto změnu naměřit?
3. Série 10. Ročníku - S. Venuše
Spočtěte ekliptikální a rovníkové souřadnice Venuše pro 24. 8. 1988 v $0^{h}UT$ (světový čas). Pro tento den určete vzdálenost Venuše od Země a máte-li doma nějakou hvězdnou mapu, určete také souhvězdí, ve kterém se Venuše nachází. Elementy drah Venuše a Země jsou:
| $a_{V}=0,72333\; \textrm{AU}$ | $e_{V}=0,00679$ | $i_{V}=3,3949^{o}$ | $\Omega_{V}=76,7112^{o}$ | $\omega_{V}=55,0804^{o}$ |
| $a_{Z}=1,00000\; \textrm{AU}$ | $e_{Z}=0,01673$ | $i_{Z}=0,0014^{o}$ | $\Omega_{Z}=352,2647^{o}$ | $\omega_{Z}=110,6756^{o}$ |
Oběžná doba Země kolem Slunce je $T_{Z} = 365,2571\; \textrm{dne}$. Údaj o okamžiku průchodu planet periheliem je nahrazen zadáním středních anomálií Venuše $M_{0}^{V}$ a Země $M_{0}^{Z}$ pro 18. 7. 1988 v $0^{h} UT$:
$$M_{0}^{V}=186,0712^{o}$$ $$M_{0}^{Z}=193,2434^{o}$$
Při řešení nepoužívejte žádné vztahy vyčtené z knih o astronomii.
2. Série 10. Ročníku - S. oběžná dráha Země kolem Slunce
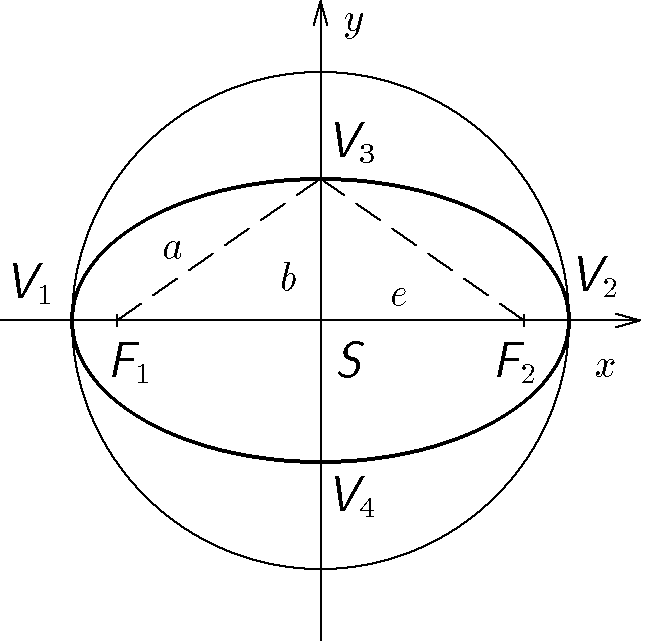
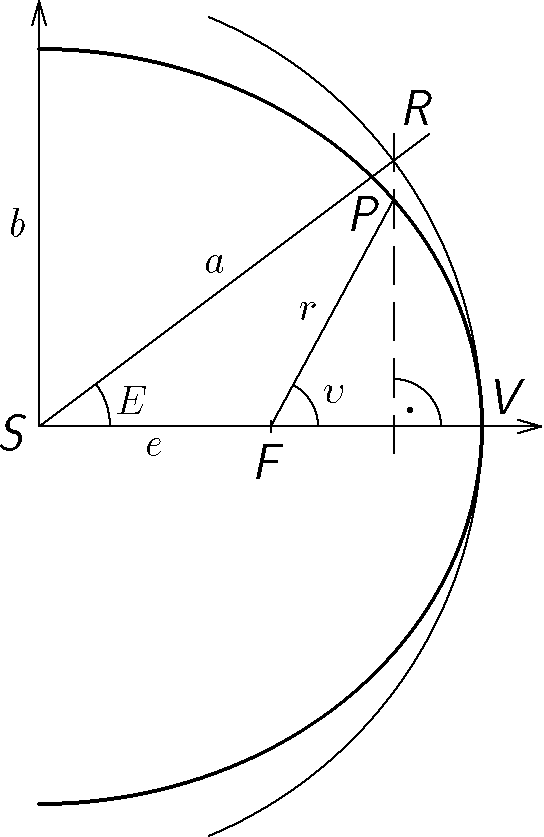
Určete pravou anomálii a vzdálenost Země od Slunce po $1/4$ oběžné doby Země kolem Slunce od průchodu Země periheliem. Velká poloosa je $a=1\;\mathrm{AU}$ a excentricita $e=0,0167$.
1. Série 10. Ročníku - S. hvězdná velikost
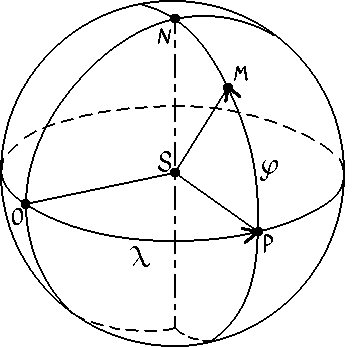
Na procvičení pojmu hvězdné velikosti si vyřešte tyto úlohy:
- Jaká je absolutní magnituda Slunce $M$, je-li jeho zdánlivá magnituda $m=-26,74$?
- Složky dvojhvězdy Castor v souhvězdí Blíženců jsou v dalekohledu jasné $m_{A}=2,0$ a $m_{B}=2,9$. Neozbrojené lidské oko však tyto hvězdy nerozliší. Jak jasná se jeví tato dvojhvězda při pozorovaní pouhým okem?
- V jaké poloze na své dráze se jeví Venuše ze Země nejjasnější? Předpokládejte, že Venuše obíhá kolem Slunce přibližně po kružnici s poloměrem $r=0,7233\;\mathrm{AU}$ a že jasnost v celé viditelné a osvětlené části povrchu Venuše je konstantní. U těch, co neumějí derivovat, se spokojíme s numerickou hodnotou vzdálenosti Venuše od Země; nakreslete si graf závislosti jasnosti Venuše na vzdálenosti a odečtete z něj polohu největší jasnosti.
- Pokuste se odhadnout jasnost Venuše v poloze, kdy je na obloze od Slunce úhlově nejdál. Albedo Venuše (tj. poměr odražené ku dopadající intenzitě záření) je $0,76$ a její poloměr $R_{V}=6052\;\mathrm{km}$. Předpokládejte, že záření odražené od Venuše se rovnoměrně rozptýlí do celého poloprostoru a že jasnost každého světlého místa viditelného povrchu bude, jako by Slunce bylo právě nad ním.
- Určete, v jaké největší a nejmenší výšce nad obzorem se v naší zeměpisné šířce nachazí Slunce během roku. Rovina ekliptiky s rovinou zemského rovníku svírá úhel $23,5$ stupňů.
6. Série 8. Ročníku - 1. Jupiter a kometa
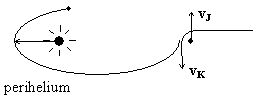
Trajektorie planety
Kometární rodina Jupiteru vzniká následujícím způsobem (viz. obrázek). Kometa přilétá k Jupiteru z velké vzdálenosti s téměř nulovou počáteční rychlostí. Po opuštění Jupiterova gravitačního pole (přesně sféry gravitačního vlivu Jupitera), má její rychlost (vzhledem ke Slunci) přesně opačný směr než rychlost Jupitera. Poté se pohybuje opět v gravitačním poli Slunce. V jaké vzdálenosti od něj se bude nacházet perihelium dráhy komety a jaká je její oběžná doba (jaká je velikost velké poloosy dráhy komety)? Uvažujte, že Jupiter obíhá kolem Slunce po kružnici o poloměru $R=5,2\;\mathrm{AU}$.
5. Série 8. Ročníku - 1. vesmírná katastrofa
Tři planetky o stejné hmotnosti $M=10^{26}\; \textrm{g}$ jsou umístěny ve vrcholech rovnostranného trojúhelníka o straně $l=100\; \textrm{Gm}$ [gigametry]. Nemajíce počáteční rychlosti nezbývá jim než padat vstříc jisté záhubě. Určete, za jak dlouho se srazí (rozměry planetek zanedbejte).
2. Série 8. Ročníku - 1. přistání kosmické sondy
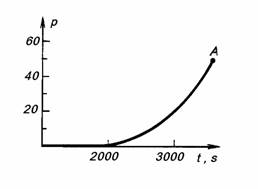
Graf závislosti
Přistávací modul kosmické lodi se přibližuje k povrchu planety s konstantní rychlostí, přičemž předává na kosmickou loď údaje o tlaku atmosféry. Graf závislosti tlaku na čase je na obrázku. Při přistání na povrchu planety modul naměřil teplotu $T=700\; \textrm{K}$ a tíhové zrychlení $g=10\;\mathrm{m}\cdot \mathrm{s}^{-2}$. Určete rychlost $v$, kterou modul přistává, když se atmosféra skládá z oxidu uhličitého. Určete teplotu $T_{h}$ ve výšce $h=12\;\mathrm{km}$ nad povrchem planety.
5. Série 7. Ročníku - P. Sluneční soustava
S nevelkou přesností pozorování (za Ptolemaia byla asi 0,5°) určil už Hipparchos vzdálenost Slunce a Měsíce, a to překvapivě dobře (59 zemských poloměrů, 134 600 000 km). Zkuste nalézt postup, jak to provedl, a odhadněte, jaká je asi chyba výsledku získaného s tehdejšími prostředky.
V šestnáctém století, stále ještě bez jakékoli optiky, se pozorovací metody značně zdokonalily (Tycho Brahe měřil s přesností na 2' ). Vymyslete, jak mohl středověký astronom určit poměry poloos drah planet vůči vzdálenosti Země od Slunce a jejich oběžné doby.
Na sféře stálic, mimo okruhy planet, se však stále jevilo nebe neměnné. Jak přesně by musel pozorovatel měřit polohy hvězd, aby zjistil jejich posuny vůči sobě, ať už skutečné nebo zdánlivé?
3. Série 7. Ročníku - P. Galileo Galilei
Usoudili jsme, že v poklidné vánoční době vás raději ušetříme přílišného počítání a naopak vyzkoušíme vaše schopnosti fyzikální argumentace bez pomoci vzorců. Za tímto účelem se tedy přenesme téměř o čtyři století zpět, do doby, kdy na univerzitě v Pise a později v Padově působil muž jménem Galileo Galilei. Nebude snad na škodu, když zde trochu přiblížíme jeho tehdejší práci a názory. Zdejší profesura ho neuspokojovala o nic více než předchozí studium, nevyhovoval mu jediný tehdy uznávaný výklad principů přírodních dějů pocházející od Aristotela. Sám se zabýval zkoumáním konkrétních vlastností hmoty, a to jak pevných těles (pevnost), tak kapalin a plynů (tlak, vakuum). Největší význam pro další rozvoj fyzikálního poznání mělo jeho studium jednoduchých mechanických systémů, kdy opustil pole statiky, zpracované již Archimedem, a pustil se do zkoumání jejich pohybových vlastností, čímž položil základy dynamiky (od něj pochází i naše pojetí pojmu setrvačnost a zrychlení). Ovšem nemenší význam měly jeho objevy učiněné na nebi, kterých dosáhl díky své vlastní zdokonalené verzi tzv. holandského dalekohledu. Počátkem 17. století je shrnul do díla nazvaného Hvězdný posel, které však bylo pro svůj kritický pohled z mnoha stran ostře napadáno. V roce 1616 pak musel sám pod pohrůžkou uvěznění upustit od svých „bludných názorů“, ve kterých se stále více blížil Koperníkovu modelu vesmírných pohybů. O osm let později, kdy nastoupil nový papež, se opět pustil do boje s nesmiřitelnou inkvizicí a vydal Dialog o obou největších soustavách světových, ve kterém obhajoval Kopernikovu představu proti všem možným argumentům opozičního tábora. Dílo podávalo daný problém tak dovedně, že po úpravách došlo i papežskému schválení.
Po vás chceme, aby jste se zamysleli se nad tím, jakých argumentů mohl při obhajobě heliocentrického názoru použíti. Uvažte dříve známé i nově objevené skutečnosti, kterými mohl Galileo svou pravdu potvrdit. Mějte na paměti, že jeho oponenty byli většinou lidé bez vědeckého vzdělání, jakož i že zakladatel matematického popisu fyzikální reality, Isaac Newton, se narodil až několik let po Galileově smrti.