Vyhledávání úloh podle oboru

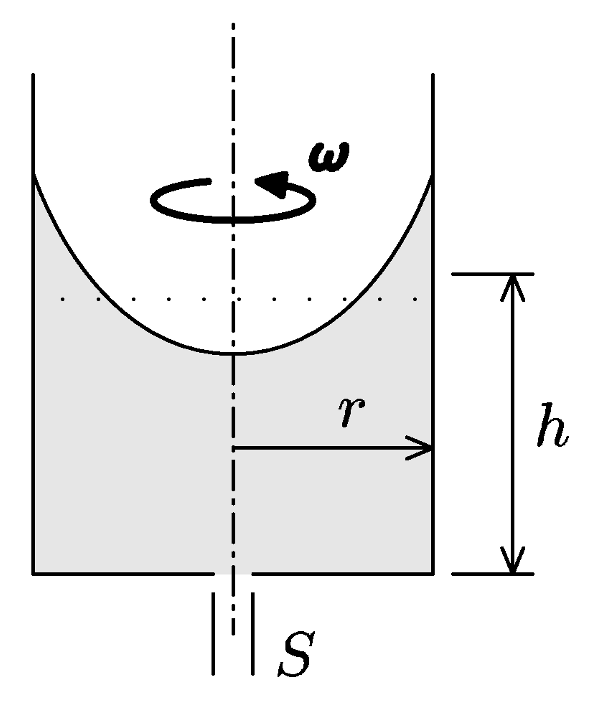
Máme dostatečně vysokou válcovou nádobu s vodou (poloměr $r$, výška hladiny vody $h)$ a roztočíme ji úhlovou rychlostí $ω$. Do středu dna uděláme malou dírku plochy $S$, přičemž nádoba stále rotuje. Kolik vody z nádoby vyteče ven?

Jak rychle musela v době tuhnutí rotovat Země, aby se rovníkový poloměr lišil od polárního právě o tolik, o kolik se liší teď?

Změřte, jak vysoko vystříkne voda při upuštění různých těles na vodní hladinu. Studujte závislost na výšce, tvaru a hmotnosti. Jaká část energie se využije na rozvlnění hladiny?

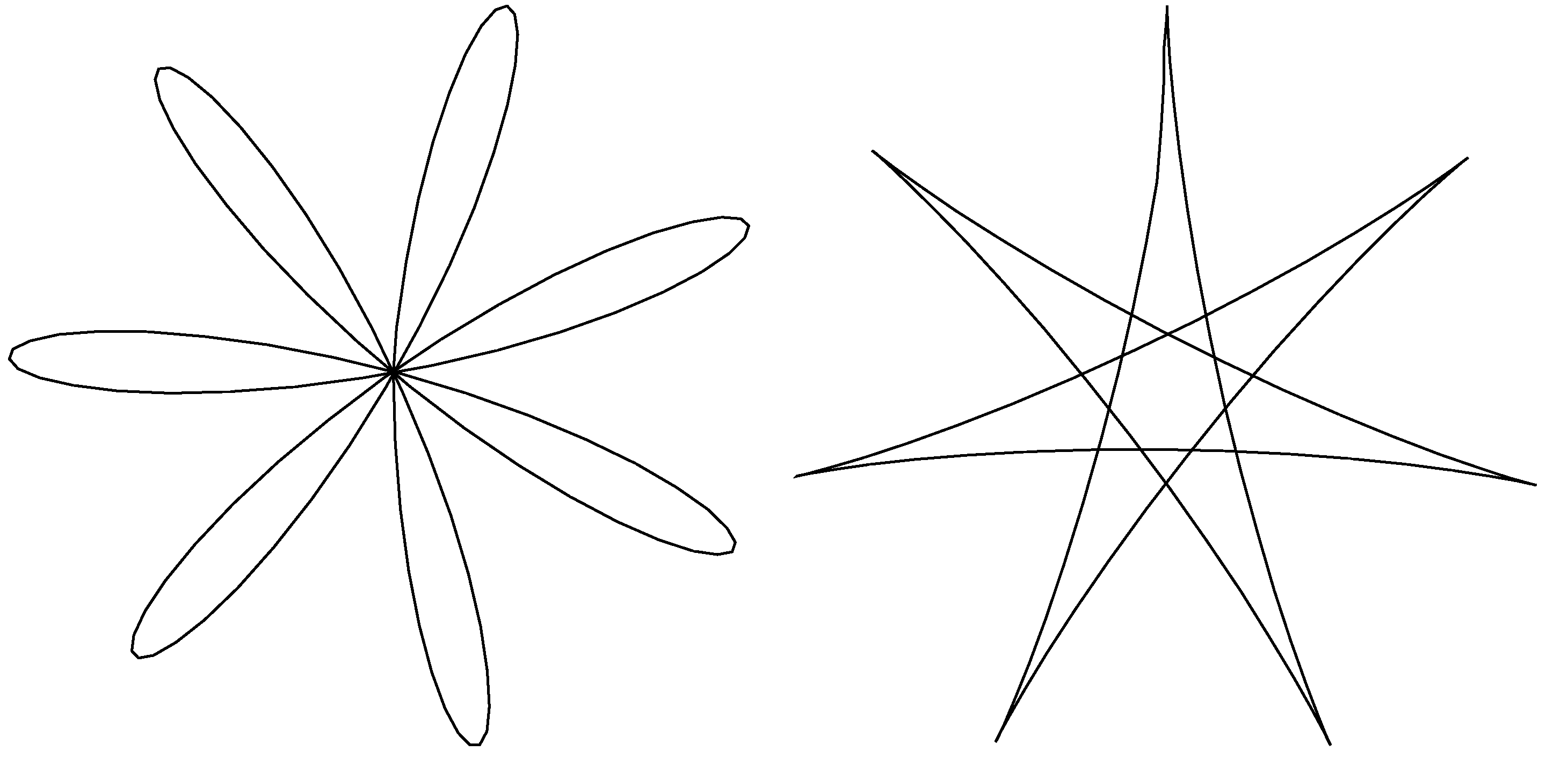
1. Foucaultovo kyvadlo do písku nakreslilo při dvou různých demonstracích dva odlišné obrazce, oba jsou na obrázku. Rozhodněte, co způsobilo jiný tvar a také jak dlouhé by muselo být kyvadlo, aby tyto obrazce mohly na podlaze pařížské katedrály vzniknout. Kolikacípé jsou hvězdy/květy ve skutečnosti?
2. Jaký tvar bude mít hladina v kbelíku s vodou, který klidně stojí na rovném stole?
3. Ukažte, že vztah

$$δf=f_{+}-f_{-}=\frac{4ωS}{λ_{0} P}$$ pro frekvenční rozdíl (frekvenci rázů) dvou protiběžných paprsků v laserovém gyroskopu platí pro jeho libovolný rovinný tvar – tedy nejen kruhový.

Organizátoři si z podzimního soustředění odvezli tlakovou nádobu s vodíkem a na vánoční besídce chtějí udělat pokus. Všechen plyn z ní vypustí do lehkého balonu – tj. bude mít atmosférický tlak. Dokáže takovýto balon uzvednout prázdnou tlakovou nádobu, když víte, že teplota zůstává konstantní?

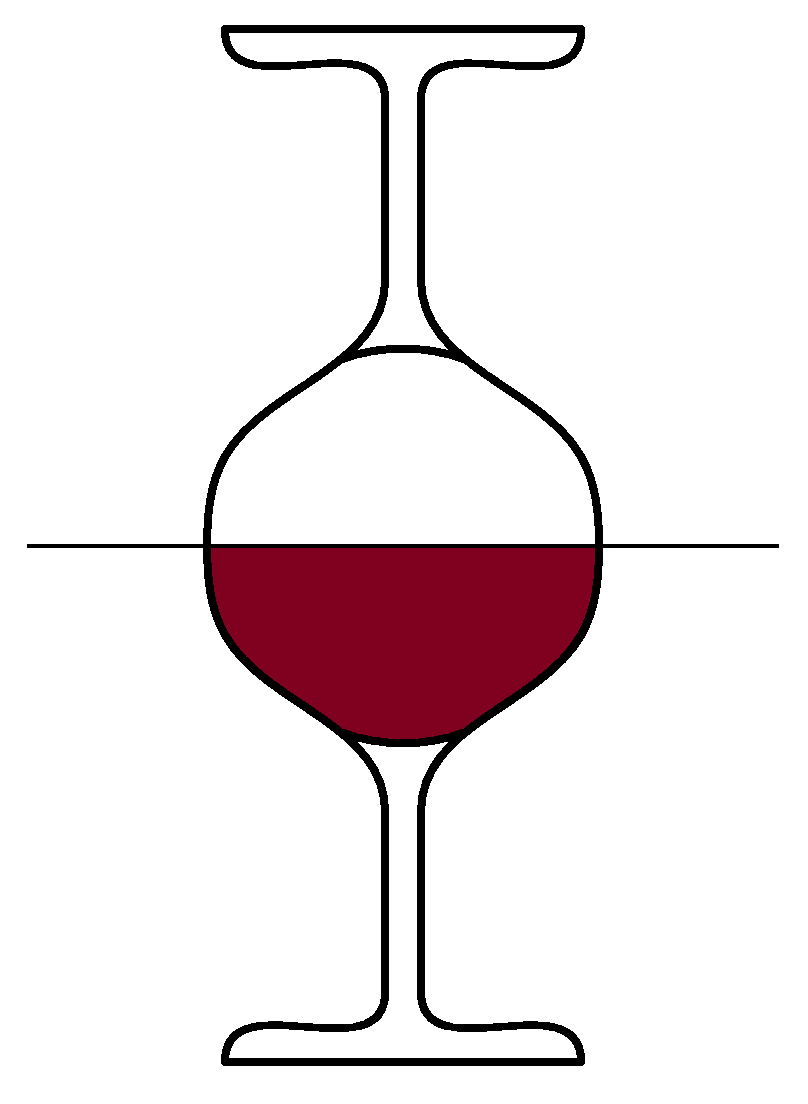
Vyzkoušejte si následující pokus. Naplňte až po okraj stejné sklenice vína a vody. Na tu s vodou položte list papíru, sklenici otočte a položte na sklenici s vínem tak, aby jejich okraje lícovaly (konečný stav vidíte na obrázku). Teď, když opatrně vytáhnete papír tak, aby v kruhu vytyčeném okrajem sklenic vznikla malá mezírka, dojde k zajímavému jevu. Obsahy sklenic se vymění, aniž by se smísily (pokus trvá poměrně dlouho, buďte trpěliví). Zkuste se zamyslet proč, ale hlavně úkaz pořádně prozkoumejte. Zjistěte, jak závisí doba výměny na ploše mezírky, koncentraci alkoholu a jiných parametrech podle vašeho uvážení. Proběhne i pro jiné kapaliny? Například pouze obarvenou vodu, mléko, olej …

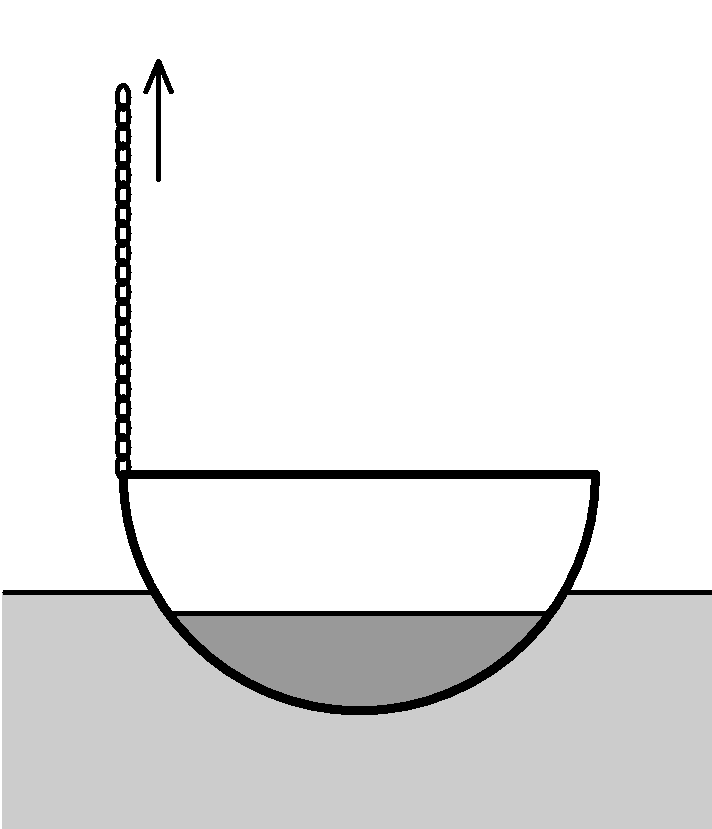
Když je hadí maso uvařené, kuchaři z něj připravují hadí polévku v měděných hrncích, které mají tvar polokoule o průměru $40\,\jd{ cm}$. Hrnec s polévkou dávají potom vychladit do nedalekého jezera. Když ho nechají plavat, ponoří se o $10\,\jd{ cm}$. K bodu na okraji hrnce je připevněn řetízek. Pokud za řetízek zatáhneme a zvedneme tak okraj hrnce o $10\,\jd{ cm}$, nateče do hrnce voda?

Příliv a odliv jsou způsobeny slapovými silami, tj. především gravitační silou Měsíce. Příliv se opakuje každých 12 hodin a 25 minut, nicméně na zeměkouli pozorujeme vždy dva přílivy na opačných stranách zeměkoule. Tzn. jeden příliv oběhne Zemi za dvojnásobek doby, tj. asi 25 hodin. Tudíž na rovníku o délce $40 000\,\jd{ km}$ se příliv musí pohybovat přibližně rychlostí $1 600\,\jd{ km ⁄ h}$. To je dokonce více než rychlost zvuku ve vzduchu.

Ze zkušenosti však víme, že voda v moři touto rychlostí neproudí, neboť lodě nám vozí banány z Kostariky atd. Je tedy nějaká chyba ve výpočtu, nebo je potřeba výsledek interpretovat jinak?

Vinaři a řidiči kamionu dobře znají šikovné přelévání kapalin z těžkých nádob. Vinař Ignác chce stočit víno z jednoho demižonu do druhého. Nejprve položí prázdný demižon na zem a plný do výšky $Δ$. Potom demižony propojí hadičkou a trochu z ní zespodu potáhne. Víno začne samovolně proudit do spodního demižonu. Za jak dlouho bude všechno víno stočeno? Předpokládejte, že demižony jsou stejné válce poloměru $R$ a výšky $H$.

Experimentálně prověřte tvrzení, že vinnou rotace Země se na severní (jižní) polokouli vír vody vypouštěné otvorem otáčí doprava (doleva). Mají-li mít vaše závěry váhu, musíte provést dostatečný počet měření v různých podmínkách.