Vyhledávání úloh podle oboru

Pokud udeříte kladivem do jednoho konce kovové tyče (jejíž průměr je mnohem menší než její délka), začnou se okolo ní šířit zvukové vlny. Narýsujte a co nejpřesněji popište, jak se bude s časem měnit tvar vlnoploch v rovině tyče. Mezi vašimi obrázky by měly být znázorněny vlnoplochy, a to v okamžicích, kdy se vlna dostala na druhý konec tyče a kdy se po odrazu vrátila opět do místa úderu. Nezapomeňte konstrukci popsat. Uvažujte pouze podélné kmity tyče. Poměr rychlosti šíření zvuku v tyči a ve vzduchu je $β=v_{tyc}⁄v_{vzduch}=10$.

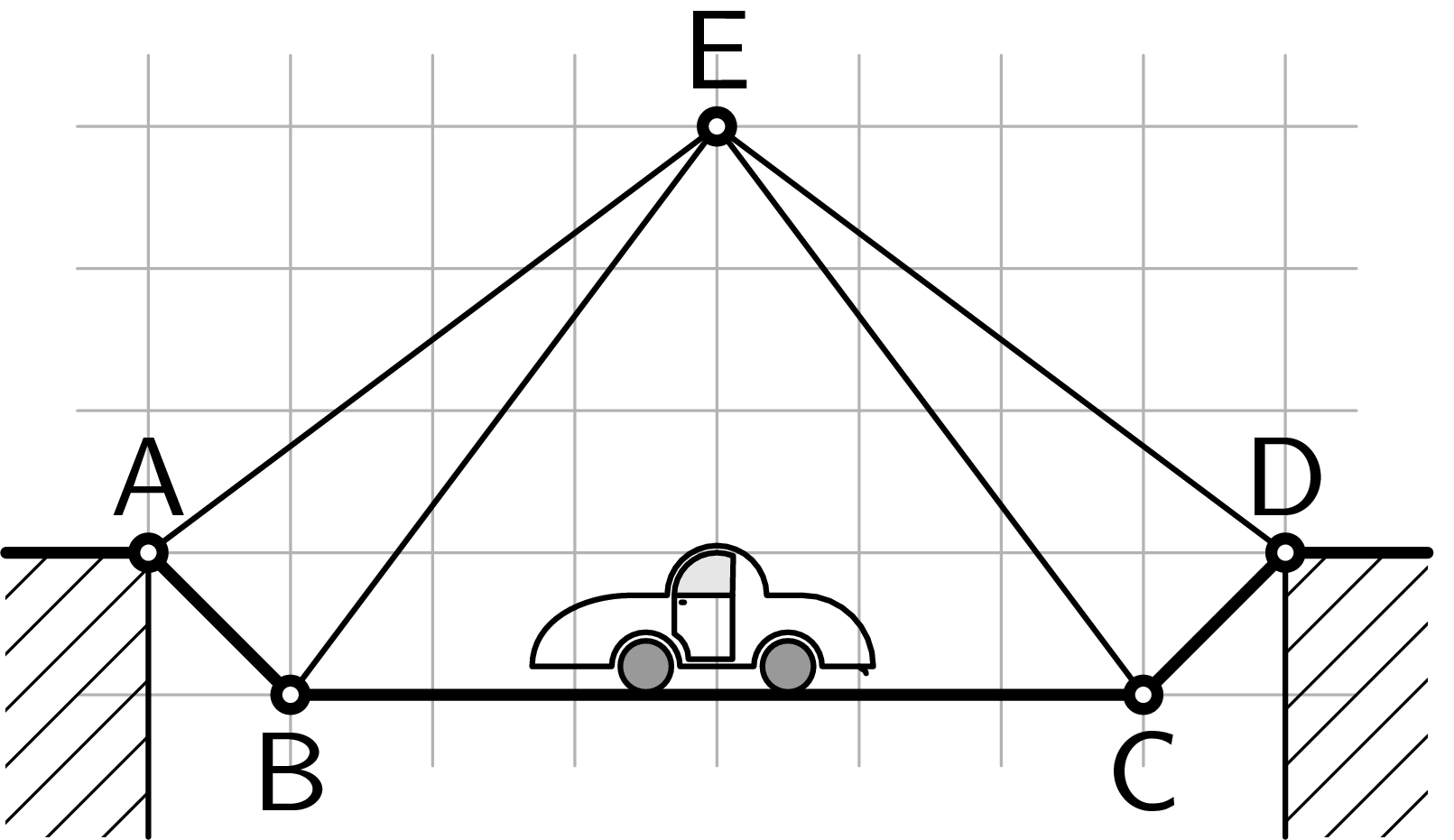
Mějme dvourozměrnou část jednoduché mostní konstrukce jako na obrázku tvořenou z tyčí spojených v bodech $A$, $B$, $C$, $D$ a $E$. Zjistěte, které tyče jsou namáhány tlakem a které tahem a jak velkými silami, pokud jsou tyče nehmotné a na tyči $BC$ stojí autíčko o hmotnosti $m$. Délky tyčí určete z obrázku.

Bonus: Uvažujte, že všechny tyče mají konstantní délkovou hustotu $λ$.

Jakou rychlostí máme jet autem z kopce, abychom co nejvíce zahřívali brzdy? Uvažujte, že rozdíl teploty vzduchu a teploty brzd je úměrný brzdnému výkonu.

Na plynovodu na daleké Sibiři, kterým teče zkapalněný zemní plyn, došlo k havárii a bylo nutné jej uzavřít. Spočítejte, jakou práci musel vykonat Váňa Vasilijevič, který byl vyslán k zásobníku zavřít výborně promazaný deskový ventil na příslušné lince. Jakou sílu musel během tohoto aktu vynakládat (vyjádřete ji v závislosti na rozumně vybrané veličině)? Ventil si představte jako desku, která je postupně vsouvána ze strany napříč do potrubí. Ve velkém rezervoáru, který je na linku připojen, je tlak $p=2\;\mathrm{MPa}$, deskový ventil má tloušťku $d=10\;\mathrm{cm}$, potrubí má čtvercový průřez o straně $a=1\;\mathrm{m}$ a zkapalněný plyn o hustotě $ρ=480\;\mathrm{kg/m}$ jím protéká s průtokem $q=20\;\mathrm{m}\;3\;\mathrm{s}$.

Změřte závislost rychlosti na čase plechovky, která je zcela zaplněná vodou a která se rozjíždí z klidu po nakloněné rovině. Použijte nakloněnou rovinu, která je dlouhá alespoň dva metry a je rovná, bez hrbolů a není prohnutá. Experiment můžete realizovat například natočením a zpracováním videí či měřením doby, za kterou plechovka sjede vždy určitý úsek dráhy.

Kdyby se všechna hmota Země vzala a přemodelovala se na kulovou slupku o tloušťce $d=1\;\mathrm{km}$ (se stejnou hustotou), jaký by tato nová „Země“ měla vnější poloměr? Jaké by bylo gravitační zrychlení na jejím vnějším povrchu?

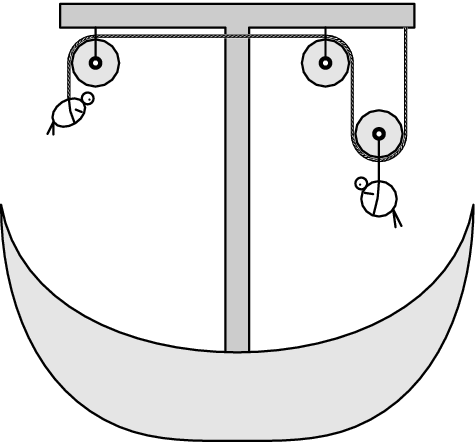
Dva mladí, ale bohužel poněkud prostorově výraznější, Benátčané Paolo a Francesca Muschetti (o hmotnostech $m_{P}=180\;\mathrm{kg}$ a $m_{F}=130\;\mathrm{kg}$) by se chtěli spolu projet na gondole. Žádný gondoliér je ale nechce vzít na svou loď, protože ví, že by je všechny tři loď neunesla. Chytrý gondoliér Jacopo ale vymyslel rampu, na kterou umístil tři kladky dle obrázku. Skrz kladky provlékl lano a oba mladé Benátčany na ně upevnil, viz obrázek – každého na opačný konec, tak, že nejprve byla nahoře lehčí Francesca a po jisté chvíli ji v této pozici vystřídal těžší Paolo. Jak vysoká musí být rampa, aby gondola stihla přejet přes kanál? Doba jízdy je $τ=60\;\mathrm{s}$. Přepokládejme, že při použití tohoto zařízení se již gondola nepotopí. Zanedbejte veškeré tření, hmotnost lana a momenty setrvačnosti kladek.

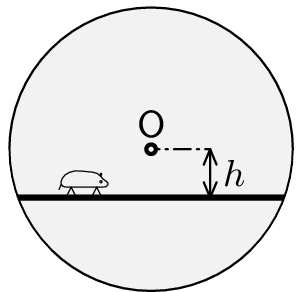
Rado si pro svého křečka Bobka přichystal speciální kolečko. Celá soustava se může otáčet okolo osy procházející bodem $O$, který je středem kolečka, a ke kolečku je vodorovně připojená deska ve vzdálenosti $h$ od osy rotace, viz obrázek. Jak se má křeček Bobek pohybovat po desce, aby deska zůstala po celou dobu pohybu vodorovně? Koeficient tření mezi křečkem a deskou je $f$.

Mějme dvě auta o stejné hmotnosti jedoucí proti sobě rychlostí $v_{0}$. V jaké vzdálenosti musí začít brzdit, aby nedošlo ke srážce? Uvažujte dva případy, kdy auta jedou proti sobě na rovině a kdy auta jedou po silnici se sklonem $α$. Víte, že oba řidiči začnou brzdit v týž okamžik a velikost brzdné síly každého auta je $f\cdot N$, kde $N$ je složka tíhy automobilu kolmá na silnici.

Pokuste se určit některé napěťové charakteristiky v tahu u lidského vlasu. Z vašeho pokusu sestavte co nejpodrobnější graf závislosti použité síly na prodloužení vlasu; z něj potom určete graf závislosti napětí na relativním prodloužení. Pokuste se z něj vyčíst/odhadnout mez pevnosti, případně i jiné charakteristiky. Měření opakujte alespoň na 3 vlasech stejné osoby.

Nápovědy. Vhodné jsou hodně dlouhé vlasy – pokud sami takové nemáte, určitě není problém takové sehnat. Průměr vlasu můžete změřit ve škole pomocí mikrometru nebo pomocí laseru. Jako závaží můžete použít mince, které mají docela dobře definované hodnoty hmotnosti.