Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
astrofyzika
3. Série 2. Ročníku - S. zeměměřiči podruhé
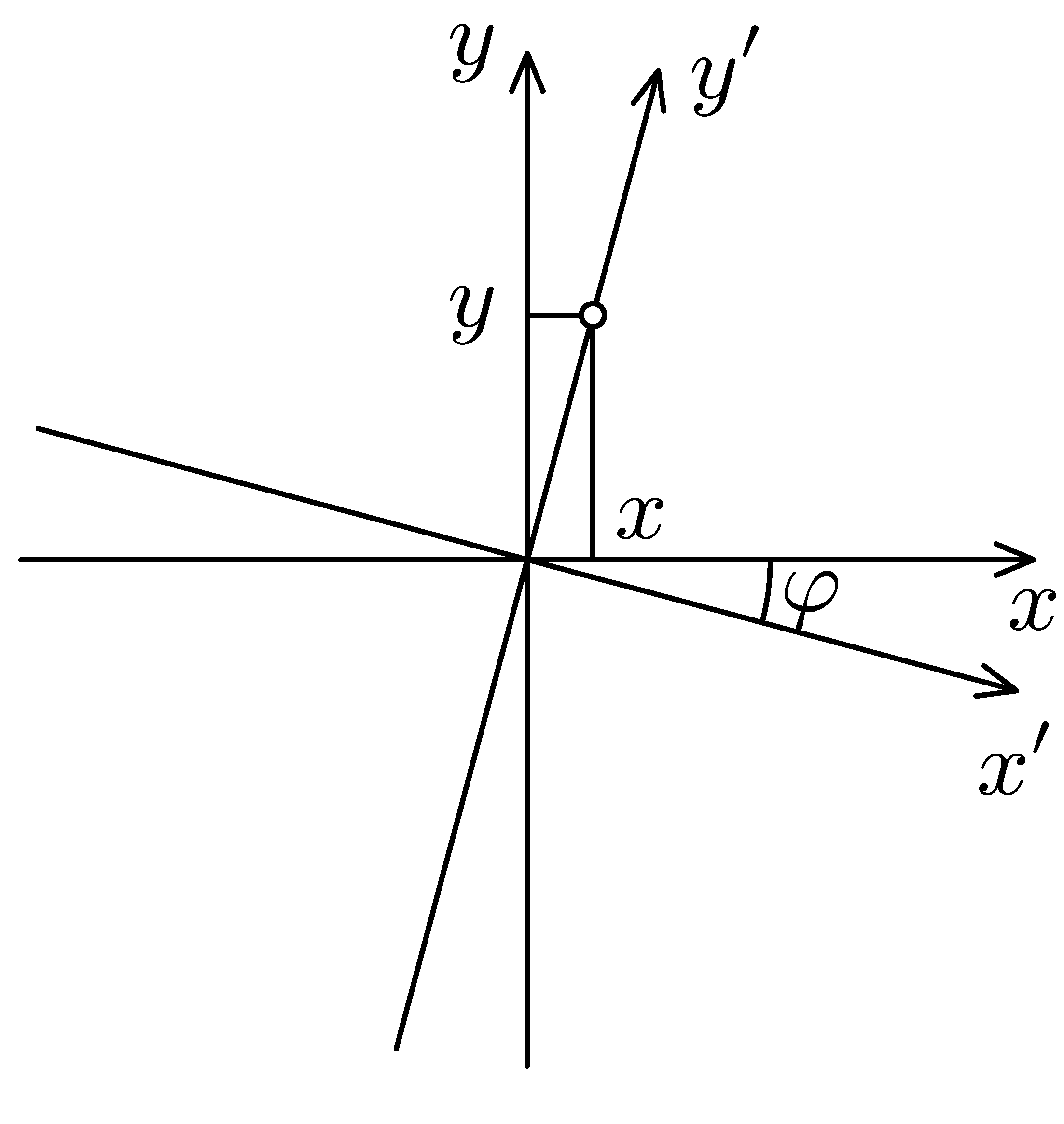
- Vraťme se opět do Severního království. V řešení příkladu I.S jste velkým zeměměřičům správně poradili převodní vzorce
$$x′=x\cos φ-yk\sin φ\; (1)$$ $$y′=kx\sin φ+y\cos φ\; (2)$$
kde $k$ je poměr metr ku severské míli a $φ$ úhel mezi magnetickým pólem a Severkou. Zeměřičům se však tento výsledek moc nelíbil, a to hned ze dvou důvodů – za prvé se v nich proti všem tradicím převádí severská míle na metr, s čímž se ale budou muset vyrovnat sami, ale hlavně za druhé neměří v Severním královstní odchylku mezi oběma používanými severními směry pomocí úhlu, ale pomocí tzv. odklonu $u$. Odklon osy $y′$ od osy $y$ je definován jako $u=x/y$, kde $x$ a $y$ jsou souřadnice bodu, který leží ve směru Severky, tj. osy $y$. Ukažte, že odklon $u$ nezávisí na tom, který bod na ose $y′$ v definici zvolíme, že odklon osy $y$ od $y′$ je $u$ a vyjádřete převodní vztahy (1) a (2) v závislosti na odklonu místo na úhlu.
- Zeměměřiči při porovnání svých výsledků zjistili zajímavou věc. Většina údajů se vlivem používání odlišných severních směrů liší, ale jeden údaj, který získávají podle vzorce $Δx+(kΔy)$, resp. $Δx′+(kΔy′)$, vychází oběma zeměměřičům stejně. Je to náhoda? Pokud ne, tak to dokažte a odůvodněte proč.
1. Série 2. Ročníku - 2. Ptolemaios a Koperník
Vraťme se ke středověkému sporu. Roku 1543 ve svém díle De Revolutionibus orbium coelestium Mikuláš Koperník předkládá svůj heliocentrický výklad světa, kterým popírá zažitou geocentrickou představu zformulovanou nejjasněji Ptolemaiem v díle Megalé Syntaxis v 2. století n. l. Umožněme myšlenkově oběma astronomům setkání, na kterém by mohli obhajovat svůj názor.
Koperník: „V mém výkladu je Slunce nepohyblivé a kolem něj se pohybují všechny planety včetně Země po kruhových drahách, což je mnohem jednodušší než popis pohybu planet v geocentrické představě.“ (Eliptické dráhy přinesl až o 60 let později Kepler.)
Co na to Ptolemaios? Kdyby byl hodně chytrý, odpověděl by třeba toto: „Tvůj názor je odvážný, mladíku, (Koperník byl o 1400 let mladší), ale myslím, že nepřináší nic nového, jenom zmatek v ustálených představách. I kdyby podle Tebe Země obíhala kolem Slunce, když se postavíme na Zemi, což stále děláme, uvidíme, že Slunce se pohybuje relativně vůči Zemi a to po kružnici. Pohyb je relativní!“ (Vskutku, pokud se nám pohyb jednoho tělesa z druhého zdá kruhový, tak opačně z prvního se pohyb druhého bude zdát opět kruhový – ověřte si to.) „Zapomeňme třeba na ostatní planety a mějme jen Slunce a Zemi. Můžeš i pak tvrdit, že Země obíhá kolem Slunce a ne naopak?“
Koperník: „Ano, i pak. Slunce stojí vůči stálicím, vůči hvězdám, a Země ne.“
Ptolemaios: „A proč by se stálice také nemohly pohybovat kolem Země? Copak Země středem vesmíru není lákavá myšlenka?“
Vidíme, že pan Koperník se dostává do úzkých. Vždyť Ptolemaios argumentuje tak revolučními a přitažlivými myšlenkami, jako že pohyb je relativní. My bychom se však přiklonili spíš ke Koperníkovi. Máme proti němu ale výhodu – víme, s čím přišel o necelých 150 let později pan Newton. Přizvěme ho k debatě. Jakými slovy vyřeší spor obou astronomů a přesvědčí Ptolemaia, zatím ale neřekneme. Co byste na místě Newtona řekli vy?
1. Série 2. Ročníku - E. sluneční čas
Jak víme, celý povrch Země je rozdělen na 24 hlavních časových pásem po 15 stupních zeměpisné délky. Na celém území naší republiky se řídíme středoevropským časem příslušejícím 15. stupni východní délky, resp. letním časem posunutým o 1 hodinu. Dále lze zavést tzv. sluneční čas, jehož poledne (12 hodin) je v okamžiku, kdy je na dané zeměpisné délce slunce nejvýše. Navrhněte metodu měření a změřte rozdíl mezi letním středoevropským časem a slunečním časem ve vaší zeměpisné délce. Výsledek porovnejte s výpočtem.
1. Série 2. Ročníku - S. zeměměřiči
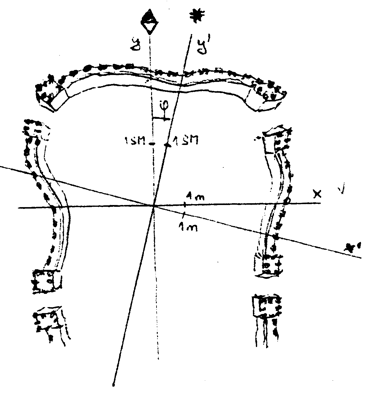
Za devatero horami v Severním království pod vládou moudrého krále žijí dva národy – denní a noční lidé. Pro potřeby obou národů zde pracují dva velcí zeměměřiči. Denní zeměměřič měří vzdálenosti k východu od středu náměstí hlavního města v metrech (označme $x$) a vzdálenosti v severním směru, který je zde považován za posvátný, měří v severských mílích ($y$). Sever určuje podle magnetky kompasu. Noční zeměměřič určuje sever podle Polárky a vzdálenosti od středu náměstí k východu opět měří v metrech ($x′$) a k severu v severských mílích ($y′$). Jednoho dne chtěli porovnat své výsledky. Ocitli se však před velkým problémem. Vzhledem k tomu, že směr k Polárce není shodný se směrem k magnetickému pólu, tak se jejich údaje liší.
- Pomozte jim a odvoďte vztahy mezi údaji $x$, $y$ a $x′$, $y′$.
- Jak by vztahy mezi $x$, $y$ a $x′$, $y′$ vypadaly, kdyby oba zeměměřiči neměřili vzdálenosti ze stejného místa?
1. Série 1. Ročníku - 2. antiraketa
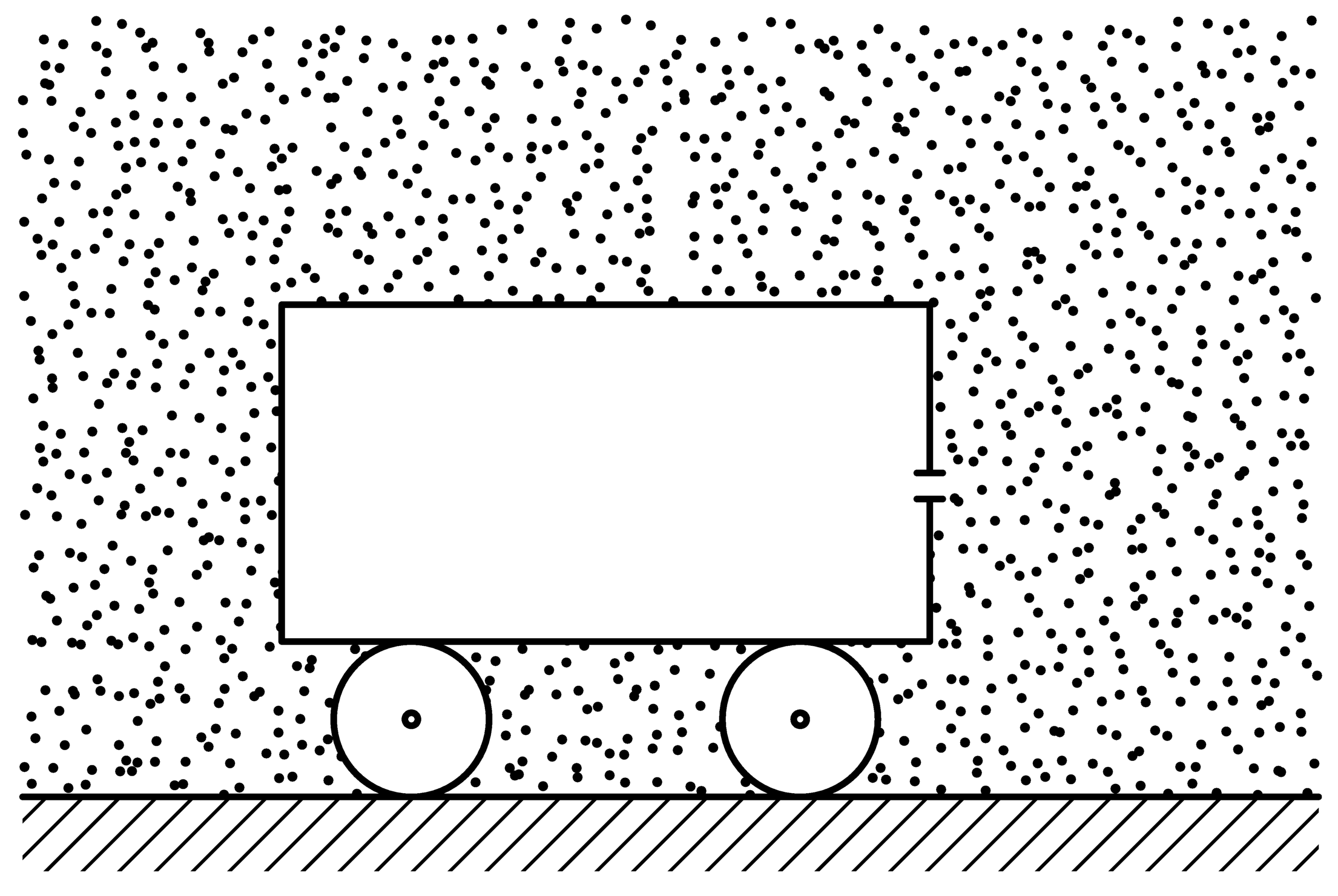
Model nádoby
Uvažujme nádobu s otvorem dle obrázku. Uniká-li stlačený vzduch z nádoby ven, nádoba se pohybuje. Jde o princip analogický raketovým motorům. Představme si nyní opačnou situaci. Nádobu, v níž bylo vakuum, umístěnou ve vzduchu, který do nádoby proudí malým otvorem. Nádoba se bude pohybovat:
- doleva
- doprava
- nebude se pohybovat