Vyhledávání úloh podle oboru

Batyskaf Trieste se ponořil do velké hloubky Mariánského příkopu a vypustil bublinu, která začala stoupat. Jakou rychlostí bude stoupat? Bude se tato rychlost měnit? Za jaký čas vystoupá až na hladinu? Jak velká je nejrychlejší bublina?

Změřte, jaký maximální podtlak (i přetlak) je člověk schopen vyvinout sáním (nafukováním) ústy.

Buffalo Bill se už roky snaží polapit Jessieho Jamese, známého banditu. V městečku Clay County mu konečně přišel na stopu. Strhla se přestřelka. Buffalo si všiml sudu plného petroleje na vozíku mezi sebou a Jessiem. „Jak dostat sud k Jessiemu, abych ho mohl zapálit,“ rozmýšlí Bill.

Jessie prostřelil sud v 9/10 výšky a ze sudu začal stříkat petrolej. Buffalo se trefil přesně do poloviny sudu a střílí znovu. Vyřešte, s jakým počátečním zrychlením se bude pohybovat vozíček v závislosti na tom, kam se Bill trefí podruhé. Předpokládejte, že hybnost kulky je nulová, a tření zanedbejte.

Do jaké výšky by se musel Buffalo trefit, aby petrolej stříkal nejdále?

Určitě jste si v super(hyper)marketu všimli, že plastová láhev oblíbeného nápoje se při rozjetí pohyblivého pásu pokladny začne otáčet a k pokladní ji často musíte postrčit až rukou. Proč to tak je?

Zkuste analyzovat následující modelový případ. Láhev je položena na pás osou kolmo na směr pohybu pásu a láhev i pás jsou v klidu. Náhle se pás rozjede konstantní rychlostí $v=10\, \jd{cm\cdot s^{-1}}$. Jakou výslednou rychlostí se bude pohybovat láhev? Nejdříve analyzujte, jak se budou chovat různé idealizace – jako třeba tuhý válec. Pak si uvědomte, že láhev je plná nápoje, který se nerad otáčí. Pro jednoduchost uvažujte viskozitu nápoje za nulovou, pak se zamyslete nad tím, jak do hry vstoupí viskozita.

Čeňkova pila se nachází na soutoku řek Vydry a Křemelné na Šumavě. Pojmenovaná je podle obchodníka s dřevem Čeňka Bubeníčka, který zde pilu v 19. století postavil. Na jejím místě nyní stojí vodní elektrárna, která je stále v provozu a patří mezi technické památky.

Vodní elektrárna využívá výškový rozdíl hladin nad a pod turbínou $10\, \rm{m}$, výkon elektrárny je $96\, \rm{kW}$. Voda je na turbínu přiváděna vantroky (Vantroky jsou dřevěná stavba – koryto obdélníkového průřezu, kterým je přiváděna voda na mlýnské kolo.), které jsou široké $1\, \rm{m}$, a voda v nich sahá do výšky $1,\!5\, \rm{m}$. Při pozorování proudící vody jsme odhadli, že uprostřed vantroků má proud vody rychlost $1\, \rm{m}\cdot \rm{s^{- 1}}$. Odhadněte, jaká je účinnost elektrárny.

Pokuste se najít libovolný vztah mezi rychlostí meteoroidu dané hmotnosti těsně před dopadem na povrch Země a poloměrem vzniknuvšího kráteru.

Na základě rozměrové analýzy najděte vztah pro rychlost vln na vodě. Teoretický vztah ověřte a najděte neznámé konstanty z měření rychlosti vln v závislosti na jejich vlnové délce. Uvědomte si, že existují dva typy vln – jedny jsou způsobené gravitací Země a druhé povrchovým napětím.

Vysvětlete, proč když zatřepeme sypaným čajem v plechovce, zůstanou větší kousky lístků spíše nahoře než dole. Řešení můžete obohatit vlastním pozorováním.

Odhadněte výšku stromů na planetě. Uvažte všechna možná hlediska, která mohou výšku stromů ovlivnit.

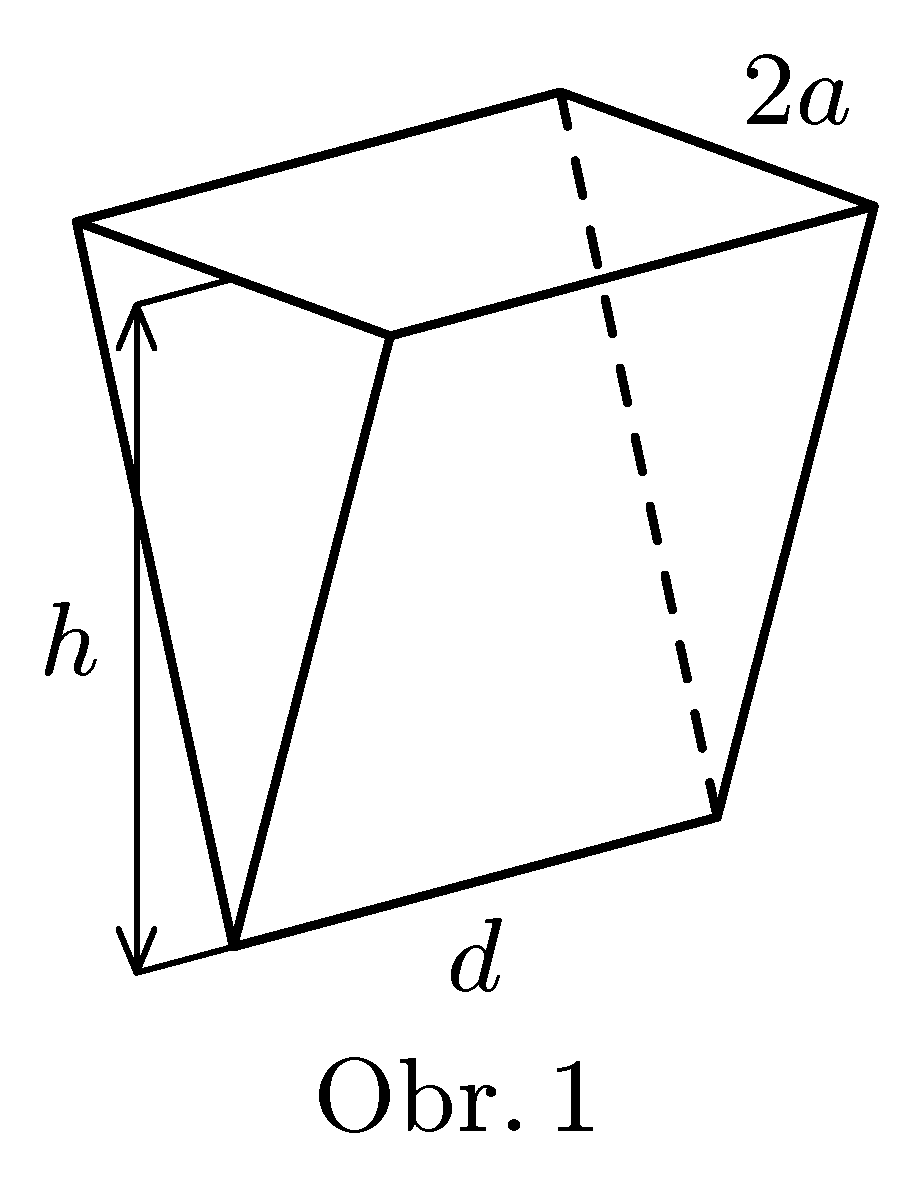
Pracovníci NASA objevili, že určité sedimenty rostlinného původu na měsíci Europa mají zajímavou štěpnost na velice pevné desky tvaru obdélníku a rovnoramenného trojúhelníku, takže z nich lze snadno a levně postavit loď výšky $h$, délky $d$ a šířky paluby $2a$ jako na obrázku 1. Kapitán vám dává za úkol zjistit, pro jaké hustoty tamějších oceánských vod bude plavba bezpečná.

Předpokládejte, že desky mají konstantní tloušťku a hustotu $ρ_{m}$, že loď je dutá a má palubu. (Diskutujte případ, že plavidlo není duté a celé má konstantní hustotu $ρ_{m}.)$ Nemusíte kapitánovi předložit jedinou výslednou relaci, spíše prakticky užitečný návod na propočty s uvedením všech potřebných vztahů; snažte se je napsat přehledně a úsporně a odůvodněte užití případné vhodné aproximace.