Vyhledávání úloh podle oboru

Odhadněte, jakou minimální rychlostí musí foukat vítr, aby odnesl papír ležící na stole.

Trať má poloměr oblouku $R$, vlak má těžiště ve výšce $H$ nad kolejemi s rozchodem $D$. Jakou maximální rychlostí může po takovéto trati jet vlak, pokud požadujeme, aby se mohl kdykoli zastavit, aniž by spadl na bok? Za jakých podmínek je maximální rychlost neomezená?

Poznámka: Zanedbejte síly působící mezi jednotlivými vagony a šířku vagonu vzhledem k poloměru oblouku.

Navrhněte způsob, jak přeměnit rotační energii Země na elektrickou energii. Fantazii se meze nekladou, konstruktéři jsou schopní a postaví všechno.

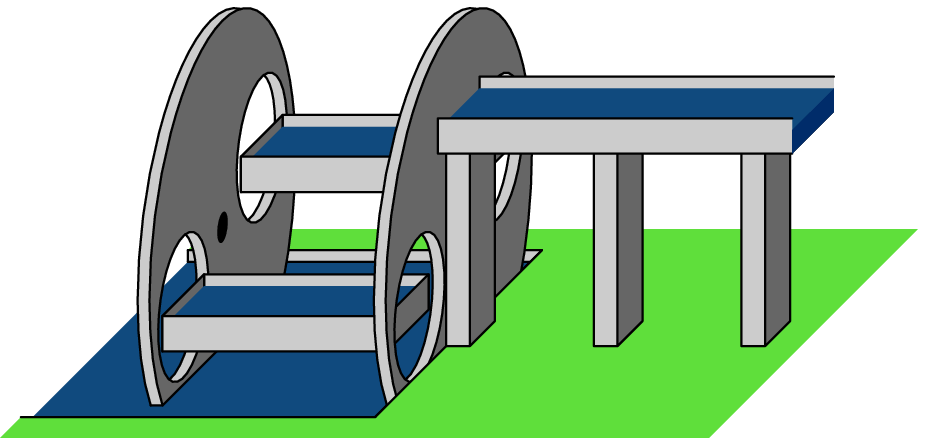
V jednom skotském městečku si postavili výtah pro lodě. Jde o dvě velké vany plné vody na koncích dlouhého ramena, které je uprostřed zavěšeno. Do vany najede loď a pomocí motoru se začne s ramenem otáčet. Jaký výkon musí mít motor, aby takto loď zvedl?

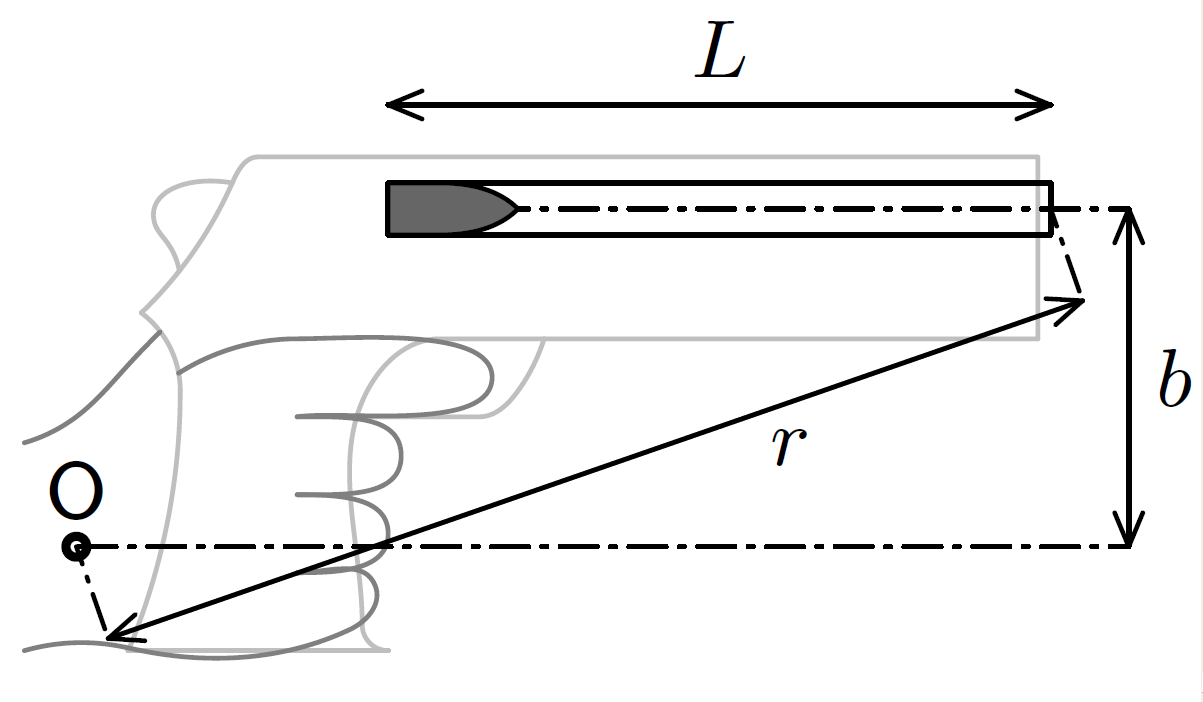
Při výstřelu z pistole zpětný ráz pistolí trhne a střela vyletí jiným směrem, než kam původně mířila hlaveň. O jak velký úhel se jedná? Uvažujte, že vliv gravitace je po celou dobu výstřelu kompenzován svaly v ruce a bod otáčení je v zápěstí. Znáte moment setrvačnosti pistole s rukou vzhledem k bodu otáčení, hmotnost a úsťovou rychlost projektilu a vzdálenosti popsané v obrázku. Hodnoty těchto veličin můžete zkusit odhadnout a výsledek číselně dopočítat.

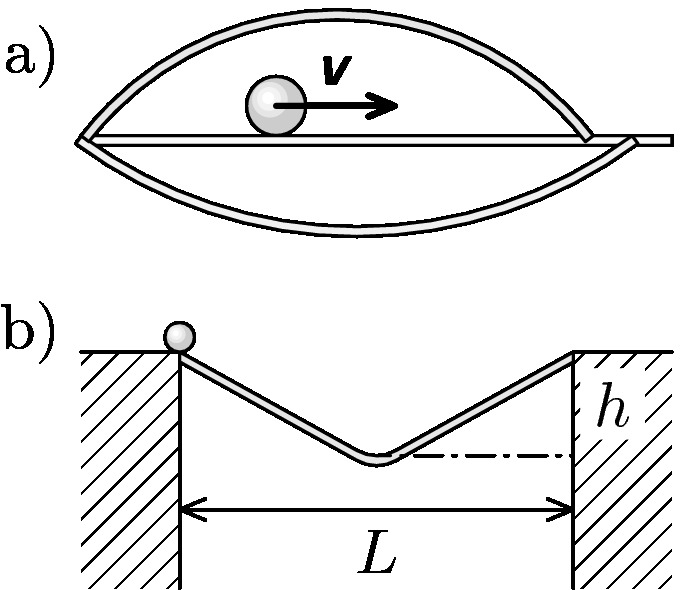
• zprohýbané prkno

Prkno dané délky leží vodorovně. Z jednoho konce po něm pošleme kuličku. Za jakých podmínek bude na druhém konci prkna nejdříve?

a) Prkno bude prohnuté nahoru.

b) Prkno bude prohnuté dolu.

c) Prkno bude rovně.

d) Při libovolném prohnutí bude doba stejná.

Svoji volbu řádně odůvodněte.

• zlomené prkno

Prohlubeň šířky $L$ přemostíme prohnutým prknem. To se skládá ze dvou stejně dlouhých rovných částí, které jsou uprostřed spojeny zlomem. Na jeden konec položíme kuličku. Pro jakou hloubku prohnutí $h$ bude kulička na druhém konci nejdříve? Zlom je tak hladký, že na něm kulička neztrácí energii. Mohlo by se vám hodit, že funkce $f(x) = x + 1/x$ má minimum v bodě $ x = 1.$

Řetěz o hmotnosti $m$ a délky $l$ visí svisle těsně nad váhou. Najednou ho upustíme z klidu a začne na váhu dopadat. Jakou váhu bude váha ukazovat v závislosti na tom jaká délka $x$ již na ni dopadla? Zanedbejte rozměry jednotlivých ok řetězu.

• napnutá struna

Frekvence kmitů napjaté struny závisí na její délce $l$, síle $F$, kterou je struna napjatá, a na délkové hustotě $ρ_{l}$. Určete z těchto údajů vzoreček pro frekvenci struny pomocí rozměrové analýzy.

• dolů

Mějme činku, jejíž závaží mají tvar disků, které jsou blízko u sebe. Tyčku omotáme jednou provázkem a činku spustíme, jak rychle padá, pokud se nesmýká? Disky mají hmotnost $m$ a poloměr $R$, tyčka je nehmotná s poloměrem $r$.

Jistě jste si všimli, že při podélném parkování zpátečkou se auto může vejít i do celkem malé mezery. Mějme auto délky $L$, šířky $d$ se vzdáleností kol $l$. Kola se mohou otočit maximálně o $α$ stupňů (tzv. „plný rejd“). Do jak velké mezery budeme schopni zaparkovat při použití zpátečky? A při parkování popředu? Jaká je ideální parkovací strategie? Auto musí být samozřejmě dokonale zarovnané v řadě (tj. rovnoběžně s chodníkem ve vzdálenosti maximálně $d_{0}$ od chodníku) a při parkovacím manévru se auto smí pohybovat pouze jedním směrem, tzn. buď dopředu nebo dozadu.

Za jakých podmínek dojde k zablokování a smýkání předního kola při brzdění, aniž bychom přeletěli přes řidítka? Jaký na to má vliv brzdění zadním kolem?