Vyhledávání úloh podle oboru

Aleš má na koleji na poličce neprodyšně uzavřenou válcovou průhlednou nádobu s toluenem, z 90 % plnou. Aleš si svůj toluen pochopitelně bedlivě střeží. Když se po víkendu vrátil na kolej, všiml si, že se hladina toluenu v nádobě o kousíček snížila a okamžitě obvinil spolubydlícího šnEka z krádeže. Až posléze si uvědomil, že o víkendu začali topit a teplota v ubikaci tudíž stoupla o 20° C. Rozřešte tento detektivní příběh a zjistěte, zda šnEk skutečně čichal toluen. Jinak řečeno: Jak velký pokles hladiny mohla způsobit změna teploty? Mohl by si takového poklesu Aleš vůbec všimnout? K řešení lze použít data uvedená na http://en.wikipedia.org/wiki/Toluene_(data_page).

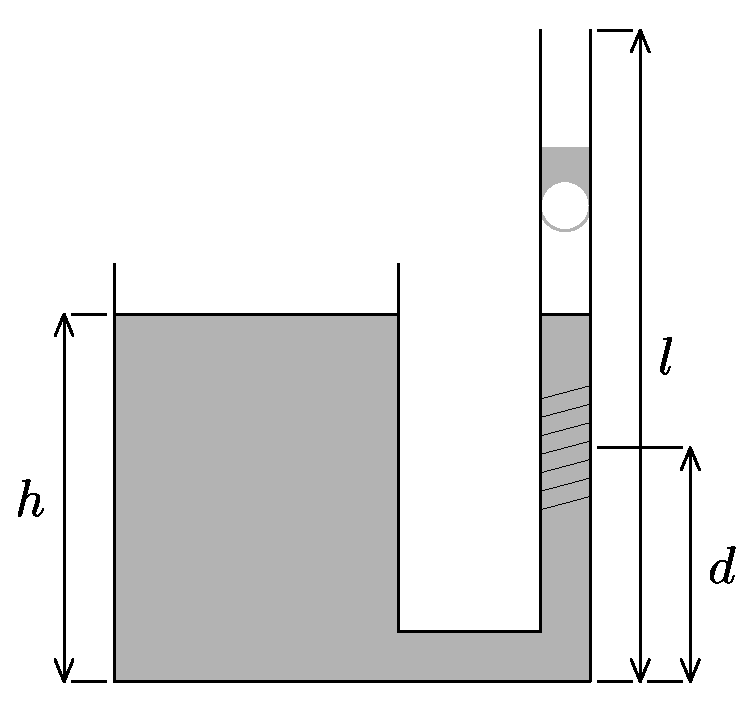
Lukáš si k psaní protokolů z praktika vařil kávu a mírně si upravil kávovar. Ke dnu nádobky přidělal zahnutou trubičku, na kterou namotal malou topnou spirálku. Spirálka byla ve výšce $d$ nade dnem nádobky (viz obrázek), hladina vody ve výšce $h$. Parametry trubičky a spirálky jsou právě takové, aby pára vzniklá varem vody přiváděné z rezervoáru v nádobce vytlačovala vodu nad sebou nahoru. Spočtěte výkon, který musíme dodávat do spirálky, aby z ústí trubičky ve výšce $l$ vytékala voda. Jaká je účinnost takovéhoto tepelného stroje?

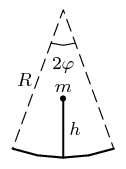
Mára si koupil bublifuk a jal se na balkoně vyfukovat bubliny, venku byl stálý atmosférický tlak $p_{0}$. Když se mu jedna obzvláště povedla (měla poloměr $r$ a hmotnost mýdlové vody byla $m)$, zamyslel se a vypočítal její celkovou tepelnou kapacitu. Učiňte totéž.

Dva světaznalí cestovatelé, jeden tlustý a jeden hubený, se cestou v letadle dohadují o tom, kdo z nich by déle přežil v extrémních podmínkách daleko od civilizace. Rozsoudíte je, kdo vydrží déle ve velkém horku (50 °C), v mrazu (-1 °C), po ztroskotání lodi uprostřed Středozemního moře, v hurikánu nebo při silném sněžení? A jak by to mohlo dopadnout, kdyby je zastihlo mohutné zemětřesení v centru velkoměsta? Kromě jejich tělesné stavby mezi nimi nejsou žádné rozdíly, oba jsou stejně oblečení a nic dalšího s sebou nemají (žádné jídlo, vodu, sirky ani jiné vybavení). Snažte se být nápadití a všímejte si i maličkostí.

Janap šla domů z hvězdárny a při pohledu na východ Slunce ji napadlo, jak by asi jednoduše šla spočítat jeho teplota. Prozradíme vám, že Země je absolutně černé těleso s teplotou $0\, \jd{^{o}C}$.

Z materiálů, které máte doma k dispozici, zkonstruujte funkční teploměr a pomocí vhodných známých teplot nakalibrujte jeho stupnici. Nezapomeňte nám poslat fotografii výsledku vašeho snažení.

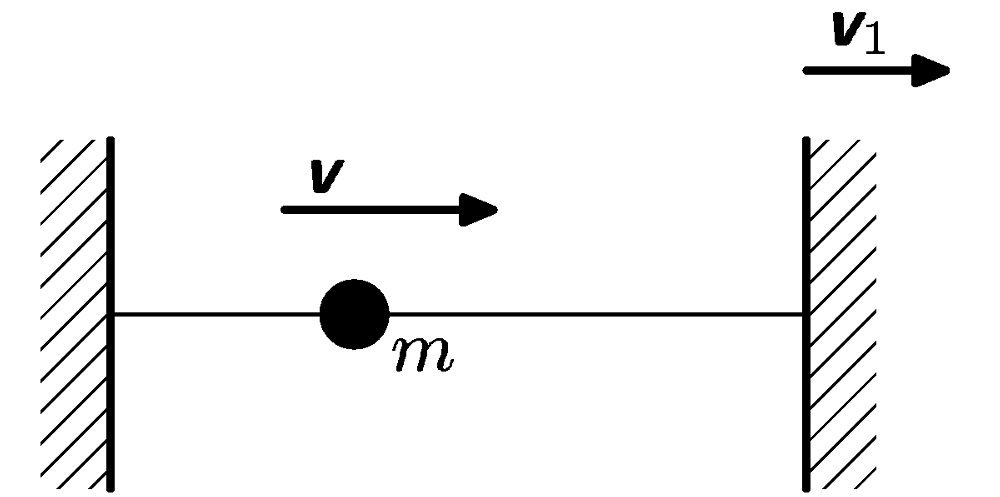
Mezi dvěma zarážkami se po přímce rovnoměrně pohybuje hmotný bod o hmotnosti $m$ rychlostí $v$. Jednu ze zarážek začneme oddalovat rychlostí $v_{1}<<v$. Jak se změní energie hmotného bodu?

Organizátoři jedou na severní pól. Mají motorové saně a i přes třeskuté mrazy okolo točny musí lít do chladiče Fridex. Poraďte jim, jakou mají volit směs alkoholu s vodou, to znamená, určete, jaká je závislost teploty tuhnutí směsi alkoholu s vodou na jeho koncentraci. Nemáte-li dostatečně výkonný mrazák, změřte, při jaké koncentraci směs zmrzne při nějaké pevně dané teplotě.

Kapilára lékařského rtuťového teploměru je pod stupnicí zaškrcená, aby se rtuť nemohla vracet do baňky a my mohli v klidu odečíst změřenou teplotu. Jak jistě víte, od června je zakázán prodej rtuťových teploměrů. Při této historické příležitosti se zamyslete, proč je zúžené místo pro rtuť průchodné pouze jedním směrem při ohřívání a proč se stejným způsobem nemůže rtuť při ochlazení zase samovolně vrátit do baňky.

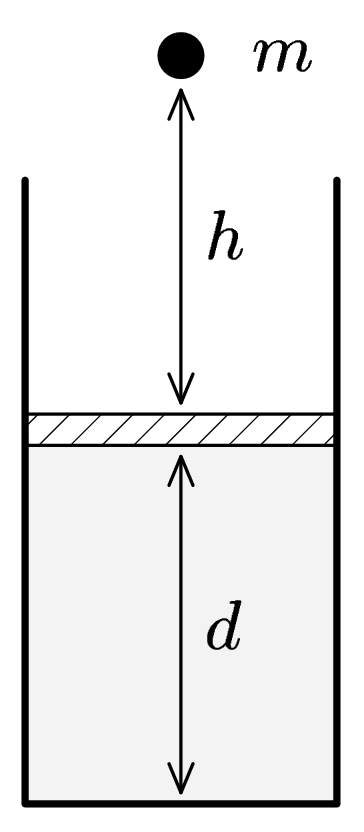
Marek má píst o rozměru $S$ s ideálním plynem v rovnovážném stavu ($p$, $V$ a $T)$. Na tento píst z výšky $h$ pustí kámen o hmotnosti $m$ (viz obrázek). Píst se stlačí a opět vrátí do nějaké polohy zpět. Jak závisí tato poloha na hmotnosti kamene a výšky, ze které byl upuštěn? Je možné, že se píst ustálí ve vyšší poloze než byl prve? Jak se změní teplota plynu v pístu?