5. Série 9. Ročníku
Termín uploadu: -
1. řetízek babičky Julie
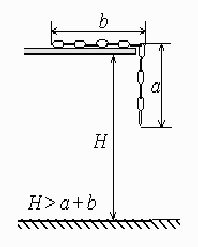
Na stole leží stříbrný řetízek po babičce Julii. Část, která je dlouhá $a$, visí přes hranu stolu, zbytek délky $b$ ještě leží na stole, jak je vidět na obrázku. Deska stolu je ve výšce $H$ nad podlahou, vše se nachází v klidu. V čase $t=0$ řetízek uvolníme a ten začne klouzat dolů ze stolu. Za jak dlouho spadne celý řetízek na zem (měřeno od chvíle, kdy se přestane dotýkat stolu)?
2. sportující elektrony
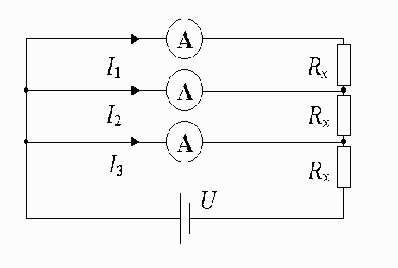
Ampérmetry na obrázku jsou všechny shodné. Odpory $R_{x}$ se také neliší svými hodnotami. Vrchní ampérmetr ukazuje hodnotu proudu $I_{1}=1\;\mathrm{mA}$, střední proud $I_{2}=4\;\mathrm{mA}$. Na spodní ampérmetr nevidíme, neboť je umístěn v ideální tmě. Baterie je plochá, tedy má napětí $U=4{,}5V$. Jaký proud $I_{3}$ teče spodním ampérmetrem a jaká je hodnota odporu $R_{x}?$
3. ucpaná roura
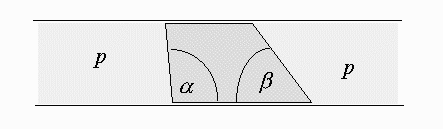
V trubce čtvercového průřezu $S$ (viz obrázek) je umístěn hranol se stěnami skloněnými o úhly $α$, $β$. Na obou stranách hranolu je plyn o tlaku $p$. Kterým směrem a s jakým zrychlením se začne hranol pohybovat, jestliže byl původně v klidu?
4. baron Prášil
Na ledovou plochu rybníka o teplotě $0\;^\circ\textrm{C}$ dopadne rozehřátá dělová koule o poloměru $R$, měrné tepelné kapacitě $c_{k}$ a teplotě $100\;^\circ\textrm{C}$. Jak hluboko se koule ponoří do ledu, jestliže měrná tepelná kapacita ledu je $c_{l}?$ Předpokládáme, že se veškeré teplo využije na tavení ledu.
P. rotující kyvadýlka
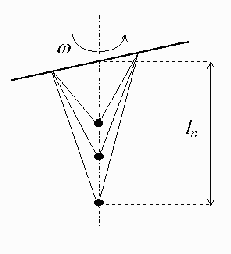
Představte si, že máte na tyčce připevněno pomocí dvou závěsů několik kuliček tak, že se mohou pohybovat po kružnici o poloměru $l_{n}$ (ve svislé rovině), kde $n$ je pořadové číslo kuličky. Potom celou soustavu roztočíme podél svislé osy úhlovou rychlostí $ω$ a nepatrně do kuliček šťouchneme (aby nebyly přímo na ose rotace). Co se děje s jednotlivými kuličkami a jak bude vypadat pohled z boku na tuto rotující soustavu?
E. experimentální úloha z mechu a kapradí
Křemílek a Vochomůrka mají problém. Uprostřed zimního spánku je probudil kapající vodovod, nenechal je usnout a nutil je přemýšlet na téma „kapající vodovody v současném světě“. Byl tak dotěrný, že pokud neumřeli, přemýšlejí dodnes. Zkuste doma objevit nějaký kapající vodovod, zamyslete se a poté změřte, jaké povrchové napětí vykazuje voda kapající z kohoutku.
S. teplotní vodivost
Ve vztahu pro tepelnou vodivost $q=Q/(S\textrm{d}t)=-\lambda(\textrm{d}T/\textrm{d}x)$ u tyče spádu teploty $\textrm{d}T/\textrm{d}x$ a průřezu $S$ a se pokuste najít vyjádření pro konstantu $\lambda$, pokud tyčí projde za čas $\textrm{d}t$ teplo $Q$.
Nápověda: střední energii jedné molekuly lze vyjádřit jako $u=m_{0}c_{v}T$.