4. Série 25. Ročníku

Eskalátory v metru na náměstí Míru mají $n$ schodů a pohybují se rychlostí $v$. Spočtěte, kolik schodů ve skutečnosti vyšlapete, pokud po nich jdete rychlostí $v_{1}$:

a) po směru jízdy,

b) proti směru jízdy.

Při pohybu proti směru uvažujte, že $v_{1}>v$.

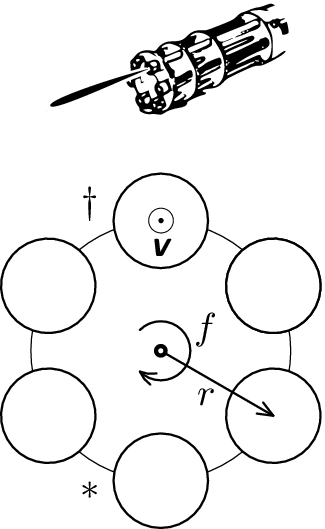
Stroj byl původně navržen pro distribuci semen do země, ale ukázal se jako mnohem užitečnější pro distribuci olova do nepřátel (rotační kulomet). Spočítejte, kde vzhledem k hlavni Gatlingu hrozí nebezpečí zasažení kulkou. Ráže je $d$, počet hlavní $n$, vzdálenost osy hlavně od osy hřídele je $r$, otáčky všech hlavní jsou $f$, kadence výstřelů je $F$ a úsťová rychlost střel $v$.

Hodíme kulatý kámen o hmotnosti $m$ z výšky $h$ nad hladinou do rybníka o hloubce $d$. Přibližně za jak dlouho spadne na dno? Jak se výsledek změní, když kámen nebude kulatý, ale placatý?

Model rakety má motůrek, jenž dává konstantní tah, dokud má palivo o počáteční hmotnosti $m_{p}$. Prázdná raketa váží $m_{0}$ a motor palivo spaluje lineárně s časem. Do jaké výšky může raketa vyletět, letí-li v homogenním gravitačním poli a zanedbáme-li odpor vzduchu?

Spočtěte, kolik procent své hmotnosti za rok ztratí zemská atmosféra, pokud uvážíte, že končí 10 \;\mathrm{km} nad zemí, po celé své výšce má konstantní tlak (stejný jako u hladiny moře), je tvořena ideálním plynem o teplotě 300 \;\mathrm{K}, splňuje Maxwellovo rychlostní rozdělení a gravitace se v jejím objemu nijak neprojevuje.

V některých bytovkách se teplá voda ohřívá centrálně pro všechny její obyvatele. V zásobníku je během dne udržována konstantní teplota vody. Šetřiví obyvatelé však ohřev na noc vypínají, voda tedy do rána vystydne a poté se opět musí ohřát. Odhadněte (na základě vyhledaných údajů), kolik energie se tímto ušetří, a navrhněte obyvatelům lepší způsoby, jak ušetřit při zachování komfortu.

Změřte účinnost rychlovarné konvice. Údaj o příkonu naleznete obvykle na samolepce zespodu konvice. Výkon určíte tak, že zjistíte, o kolik stupňů Celsia se zahřál daný objem vody za jednotku času. Pokuste s se minimalizovat chybu měření a popište, jak jste se toho snažili dosáhnout.

Varování: Rozhodně sami nepoužívejte voltmetr a ampérmetr u takto vysokého napětí a proudu.

• Spirální galaxie můžeme velmi hrubě popsat logaritmickou spirálou $r(\phi)=r(0)\exp(\phi\tan Φ)$, kde $r$ a $φ$ jsou polární souřadnice a $Φ$ je úhel otevření odpovídající úhlu, který svírá kolmice k průvodiči s tečnou ke spirále (úhel otevření roste ve směru hodinových ručiček, vyjadřujeme jej v radiánech, přičemž hodnota může nabývat více než $2π$). Uvažujme $Φ = 10°$. Odvoďte vztah pro poměr vzdáleností dvou sousedních závitů téhož spirálního ramene od centra galaxie. Jak by se poměr změnil, kdyby ramena byla čtyři (rovnoměrně rozložená). Vyjádřete vzdálenost pro sousední ramena v $r(0)=8 \;\mathrm{kpc}$.

• Uvažujte nekonečný vesmír s konstantní hustotou hvězd a bez extinkce. Vyjádřete vztahy pro integrální a diferenciální počet hvězd v závislosti na zdánlivé hvězdné velikosti. Co se stane, bude-li zdánlivá hvězdná velikost velká?

• Bonus: Jaká je pravděpodobnost, že dvě hvězdy se nám v galaxii promítnou za sebe? Uvažujte osamocené hvězdy, ne dvojhvězdy.