3. Série 24. Ročníku

• Dr. Nec

Terka byla o víkendu tahat dřevo. Objem dřeva se měří dvěma způsoby: na kubíky (1 m dřevo-hmoty bez vzduchových mezer mezi kládami) a na plnometry (1 m i s mezerami). Nalezněte převodní vztah mezi těmito dvěma jednotkami (tj. kolik plnometrů odpovídá jednomu kubíku) v závislosti na poloměru klád, ze kterých se skládá hranice. Klády považujte za dokonale hladké válce, které se skládají na sebe.

• bublifuk

Foukáme do mýdlového povrchu na počátku kruhového tvaru tak, aby měl tvar kulového vrchlíku o poloměru $r$. Odhadněte, jakou rychlostí do něj musíme foukat?

Jistě jste si všimli, že při podélném parkování zpátečkou se auto může vejít i do celkem malé mezery. Mějme auto délky $L$, šířky $d$ se vzdáleností kol $l$. Kola se mohou otočit maximálně o $α$ stupňů (tzv. „plný rejd“). Do jak velké mezery budeme schopni zaparkovat při použití zpátečky? A při parkování popředu? Jaká je ideální parkovací strategie? Auto musí být samozřejmě dokonale zarovnané v řadě (tj. rovnoběžně s chodníkem ve vzdálenosti maximálně $d_{0}$ od chodníku) a při parkovacím manévru se auto smí pohybovat pouze jedním směrem, tzn. buď dopředu nebo dozadu.

Aleš má na koleji na poličce neprodyšně uzavřenou válcovou průhlednou nádobu s toluenem, z 90 % plnou. Aleš si svůj toluen pochopitelně bedlivě střeží. Když se po víkendu vrátil na kolej, všiml si, že se hladina toluenu v nádobě o kousíček snížila a okamžitě obvinil spolubydlícího šnEka z krádeže. Až posléze si uvědomil, že o víkendu začali topit a teplota v ubikaci tudíž stoupla o 20° C. Rozřešte tento detektivní příběh a zjistěte, zda šnEk skutečně čichal toluen. Jinak řečeno: Jak velký pokles hladiny mohla způsobit změna teploty? Mohl by si takového poklesu Aleš vůbec všimnout? K řešení lze použít data uvedená na http://en.wikipedia.org/wiki/Toluene_(data_page).

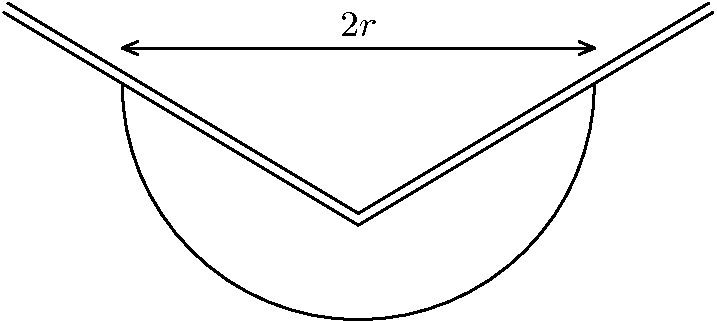
Uvažujme misku o poloměru $r$, do které položíme dvě spojená brčka, která mají tvar písmene V. Brčko se smí dotýkat pouze okrajů misky. Určete nejprve podmínku stability a potom vypočítejte periodu kmitů brčka v souměrné poloze.

Voda má spoustu zajímavých, výjimečných a anomálních vlastností ve srovnání s jinými kapalinami. Podrobný výčet těchto anomálií lze nalézt na stránce http://www.btinternet.com/ martin.chaplin/anmlies.html. Zamyslete se, jaký tyto anomálie mají význam pro život na zemi, člověka a také techniku.

Změřte, jak závisí průsvitnost papíru na úhlu, pod kterým je sklopený. Máme soustavu oko papír žárovka v jedné přímce. Měříme závislost intenzity prošlého světla na úhlu stočení papíru vzhledem k ose aparatury.

• Dopočtěte fyzikální význam konstanty $a$ pro funkci $f(z)=a\rm{i}⁄z$, znáte-li délkovou hustotu náboje $τ$.

• Vypočítejte a nakreslete ekvipotenciály a silokřivky pole v okolí rohu,

který má vrcholový úhel $θ$.

Nápověda: použijte funkci tvaru $w(z)=Az^{s}$, kde $s$ je vhodná reálná konstanta.

• Určete pole, které generuje elektrický dublet. Dublet jsou dvě tyče vzdálené $d$ s opačnou nábojovou hustotou, přičemž

$dτ=\;\mathrm{konst}$. Zajímá nás limita $d→0$.

Nápověda: platí ln$(1+x)≈x$ pro $x$ blízké 0.

• Rozmyslete si, co se stane, pokud existující komplexní potenciál $w(z)$

zobrazíme jinou holomorfní funkcí $v(z)$. Bude potenciál tvaru $v(w(z))$ i nadále řešit rovnice elektrostatiky?