3. Série 8. Ročníku
Termín uploadu: -
1. zasněžená
Malý Bobeš přitáhl pod kopec sáňky. Hledí na jeho vrchol, který je o $h$ metrů výše než on a vzdálený (vodorovně) $l$ metrů. Těžké sáňky o hmotnosti $m$ drhnou na čerstvém sněhu s koeficientem tření $f$. Přemýšlí, při jakém tvaru svahu by se dostal nahoru s vynaložením nejmenší práce. Co mu poradíte (dřív než tam zmrzne, filosof jeden)? Zkuste tuto práci pro zvolený tvar svahu také vypočítat.
2. kostka
Nalezněte tvar čela vlny na hladině rybníka, do něhož jsme vhodili pravidelný hexaedr (tj. šestistěn, pro neznalé krychle) o hraně $a$ tak, že dopadla na hladinu jednou svou stěnou. Jak bude tato vlnoplocha vypadat ve vzdálenosti $r\gg a$?
3. polytropa na zahřátí
Pod pojmem polytropický rozumíme v termodynamice proces charakterizovaný rovnicí $pV^{α}=\;\mathrm{konst.}$, kde $α$ je daný parametr. Pro vhodné $α$ dostáváme např. izobarický ($α=0$), izotermický ($α=1$) nebo izochorický ($α=∞$) děj. Mějme nejjednodušší případ ideálního jednoatomového plynu. Při jakém polytropickém ději (t.j. pro jakou hodnotu $α$) se v něm zachovává
- počet srážek atomů v jednotce objemu
- celkový počet srážek?
4. odpor 4-rozměrné krychle
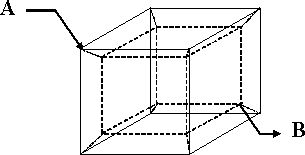
Model 4-rozměrné krychle
Představte si krychli ve čtyřrozměrném prostoru, jejíž hrany jsou tvořeny odpory $R$ (pomůckou vám bude obrázek, který zachycuje ekvivalentní zapojení ve třech dimenzích znázorněné na dvourozměrném papíře). Vaším úkolem je spočítat výsledný odpor mezi body na tělesové úhlopříčce (mezi levým horním předním vnějším rohem na obrázku – bod $A$ a pravým dolním zadním vnitřním rohem – bod $B$). Zdá-li se vám to příliš snadné, pokuste se zobecnit výsledek pro libovolnou hodnotu dimenze $n$ (a případně určete k jaké hodnotě se jejich odpor blíží pro $n$ rostoucí k $∞$).
E. grant strýčka Skrblíka
Vašim milovaným strýčkem vám byl zadán úkol zjistit, zda jeho památeční rodinná lžička jest skutečně z ryzího hliníku. Vaše experimentální vybavení je však poněkud skromné: kromě uvedené lžíce dostanete k dispozici závaží o známé hmotnosti, dlouhé pravítko, provázek a dva hřebíky, které můžete zatlouct do zárubně dveří. Navíc zde ještě stojí kbelík plný vody. Navrhněte, výpočty podložte a hlavně proveďte měření, při kterém co nejpřesněji s pomocí jmenovaných pomůcek určíte hustotu materiálu lžičky. Uskutečněte dostatečné množství měření a na základě alespoň nějakých kalkulací také odhadněte věrohodnost vámi obdrženého výsledku.
Nápověda: Pokuste se srovnat hmotnost lžíce a závaží zavěšováním na provázek, který jste (s mírným průvisem) natáhli mezi zárubní dveří.
S. trochu jiná metoda
Upravte program uvedený v minulé sérii z metody regula falsi na metodu sečen a zjistěte, jak se zrychlí konvergence metody na stejném příkladu jako v minulé sérii. Úlohu uvažujte čistě kinematicky, bez počítání hybností a sil: deska kmitá jako volný harmonický oscilátor a skokan se pohybuje jako hmotný bod ve svislém vrhu. Ověřte, jak mnoho je nyní konvergence závislá va volbě výchozího bodu. Pokuste se metodu zrychlit pomocí Aitkinova procesu: vždy po třech přiblíženích spočtených bežným způsobem proveďte extrapolaci k řešení $γ$. Jak se uvedený postup vyplatí při metodě regula falsi a při metodě sečen?