5. Série 11. Ročníku
Termín uploadu: -
1. dvojpíst
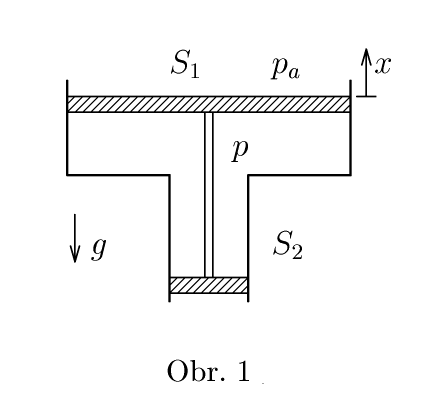
Píst
Na obrázku obr. 1 vidíte dva spojené písty o ploše $S_{1}$ a $S_{2}$ a celkové hmotnosti $m$ zasunuté do pouzdra, které je na obou stranách otevřené. Celé zařízení je v rovnováze a je umístěno v tíhovém poli $g$. Vně pístů je atmosférický tlak $p_{a}$, uvnitř je $1\,\jd{kmol}$ ideálního plynu o tlaku $p$. O kolik stupňů Celsia musíme plyn mezi písty ohřát, aby se písty posunuly o $x$ směrem vzhůru?
2. hradní studna
Řešitel FYKOSu měřil hloubku hradní studny. Vzal si na pomoc stopky a kámen. Kámen vhodil do studny a současně spustil stopky. Zastavil je poté, co uslyšel náraz kamenu na dno. Stopky ukázaly údaj $4,77\,\jd{s}$. Jelikož si náš přítel pamatoval velikost tíhového zrychlení a rychlost zvuku, ihned na místě spočítal hloubku (vyschlé) studny. Dokážete to také? Určete zároveň chybu popsaného měření.
3. kapacitní krychle
Spočítejte kapacitu krychle, jejíž hrany jsou tvořeny kondenzátory o kapacitě $C$. Uvažujte všechna tři možná zapojení krychle do obvodu.
4. cvičená opice
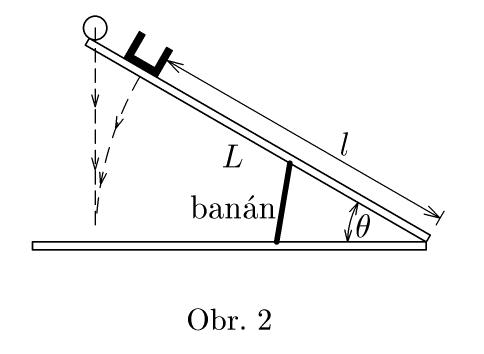
Konstrukce atrakce
Novopečený majitel zoologické zahrady by měl rád v pavilonu opic následující atrakci. Na jednom ze dvou prkýnek spojených pantem je ve vzdálenosti $l$ od pantu připevněn miniaturní košíček a na konci prkýnka (ve vzdálenosti $L$ od pantu) je položen míček. Prkýnko je podepřeno banánem, a svírá se zemí úhel $θ$. K této „aparatuře“ přijde hloupá opice (zatím nebyl čas ji vycvičit), a vezme si banán.
Vyvrcholením atrakce by mělo být to, že odbrzděné prkénko se dá do pohybu a míček by měl sám spadnout do košíčku. Diskutujte, zda-li je to vůbec možné a pokud ano, spočtěte jaké musí být $l$ v závislosti na $L$ a úhlu $θ$.
P. samopal
Rozhodněte jak těžkou krychli lze převrátit střelbou ze samopalu (či spíše menšího děla) o parametrech 50 střel za sekundu, rychlost střely $500\, \jd{m. s^{-1}}$, hmotnost střely $100\,\jd{ g}$. Krychle má hranu dlouhou $1\,\jd{m}$, po podložce neklouže.
E. pevnost nitě
Změřte mez pevnosti nitě v tahu. S řešením nám pošlete $1\,\jd{ m}$ dlouhý vzorek vaší nitě.
S. srážky a rozpady částic
- Pion $π^{0}$, který byl v laboratorní soustavě v klidu se rozpadnul na dva fotony:
$$π^{0} → γ + γ.$$
Vypočítejte jejich energie.
- Uvažujme rozpad pionu $π^{+}$, který byl v laboratorní soustavě také v klidu, na antimion a mionové neutrino:
$$π^{+ } → μ^{+} + ν_{μ}.$$
Zjistěte energii tohoto neutrina za předpokladu, že jeho klidová hmotnost je nulová. Při výpočtu je výhodné použít zákona zachování energie a hybnosti a rovnici $E^{2}-p^{2}c^{2}=m_{0}^{2}c^{4}$.
- Pokud mají dva elektrony dostatečně velkou energii, může se při jejich srážce zrodit elektron-pozitronový pár:
$$e^{-} + e^{-} → e^{-} + e^{-} + e^{-} + e^{+}.$$
Určete, jakou minimální energii a rychlost musí mít první elektron v laboratorní soustavě, pokud je druhý elektron v téže soustavě v klidu.
Uvažte, že v mezním případě se při pohledu z těžišťové soustavy srazí dva elektrony s opačnými hybnostmi a všechny čtyři výsledné částice pak zůstanou prakticky stát.