3. Série 31. Ročníku
Termín uploadu: 9. 1. 2018 23:59:59
(3 body)1. zpomalená
Představme si, že na kameru se snímkovou frekvencí 24 snímků za sekundu (uvažujme časově rovnoměrně rozložené a dokonale ostré snímky) natočíme let vrtulníku s otáčkami hlavního rotoru $2 900 \mathrm {ot./min}$. Následně si záznam přehrajeme. Jaká bude zdánlivá frekvence otáček rotoru na záznamu?
Michal se díval z okna koleje na vrtulník.
(3 body)2. zrychleníčko, zrychlení
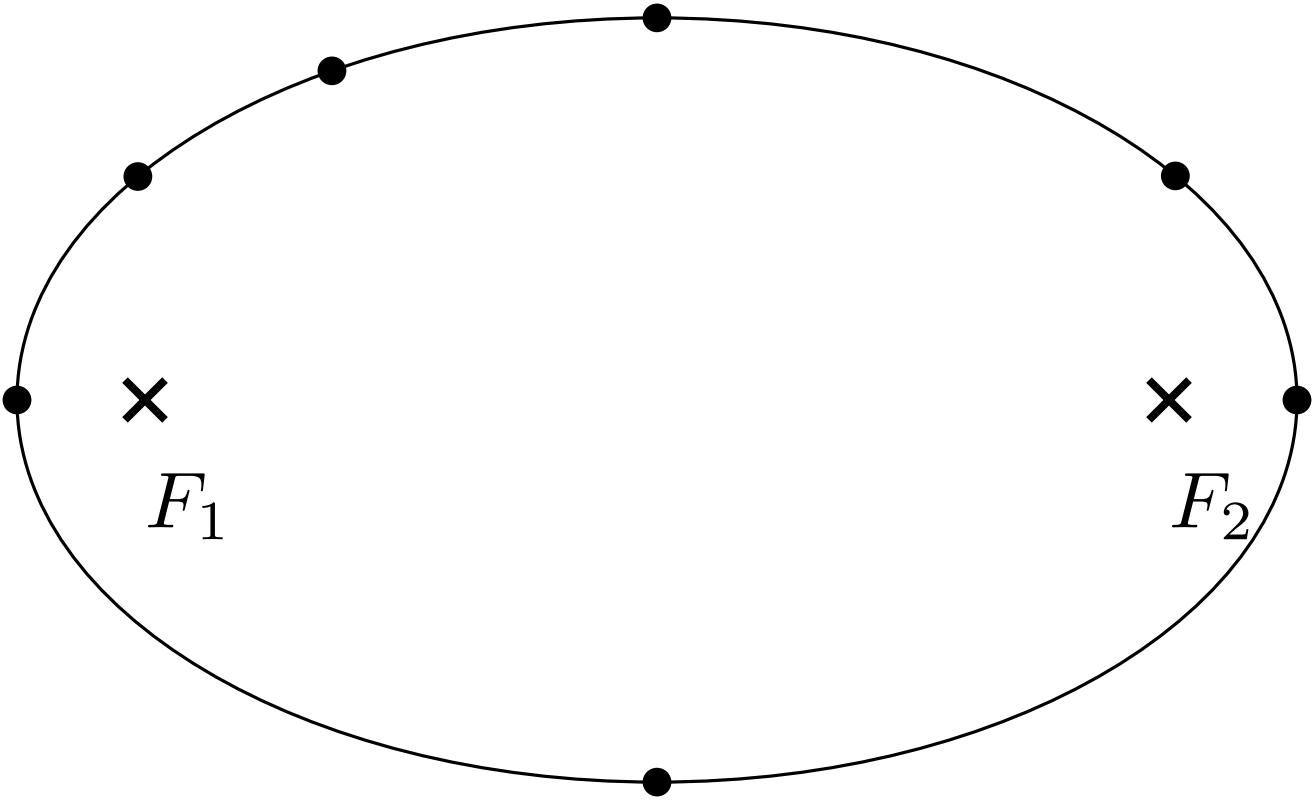
Náčrt elipsy
Na obrázku vidíte náčrt elipsy s ohnisky $F_1$ a $F_2$ a několika vyznačenými body na ní. Uvažujte, že elipsa znázorňuje trajektorii nějakého hmotného bodu. Znázorněte do obrázku zrychlení, která působí na hmotný bod v jednotlivých vyznačených bodech dráhy pro dvě situace (jde o směry a vzájemné poměry zrychlení (které je větší/menší) v různých bodech v rámci jednoho náčrtu).
- V ohnisku $F_1$ je umístěno hmotné těleso, kolem kterého hmotný bod obíhá. Uvažujeme, že platí 2. Keplerův zákon.
- Těleso má konstantní velikost rychlosti, pouze se pohybuje po elipse.
Karel na konferenci slyšel, že s takovými úlohami mají problémy i vysokoškoláci.
(6 bodů)3. IDKFA
Vypálili jste na impa z plazmové pušky, která střílí stabilní shluk částic s rovnoměrným rozdělením podélné rychlostí v intervalu $\langle v_0, \; v_0+\delta v\rangle$ (příčná rychlost je nulová) a s celkovou energií $E_0$. Hlaveň pušky má průřez $S$ a pulz trvá nekonečně krátký čas. Jak daleko musí imp stát, aby se mu nic nestalo? Předpokládejte, že jeho kůže bez problémů uchladí na malém prostoru tepelný tok $q$.
Příklad byl mírně pozměněn, neboť jsme neodhadli jeho náročnost.
Na DOOMa si vzpomněl.
(7 bodů)4. upuštěná propiska
Propisku (tuhou tyč) upustíme na stůl tak, že během svého letu svírá úhel $\alpha $ s vodorovnou rovinou. Jakou rychlostí dopadne její druhý konec (ten, co se stolu dotkne jako druhý), jestliže jsme těžiště upustili z výšky $h$? Všechny srážky jsou nepružné a tření mezi stolem a koncem propisky dostatečně velké.
Bonus: Spočítejte, jaký musíme zvolit úhel $\alpha$, aby druhý konec dopadl s co nejvyšší rychlostí. Pro jaké výšky se vyplatí propisku naklonit?
Matěj se nudil.
(8 bodů)5. rozpad sem, rozpad tam
Máme $A_0$ částic typu $A$, které se s rozpadovou konstantou $\lambda \_A$ rozpadají na částice typu $B$. Ty se zase s rozpadovou konstantou $\lambda \_B$ rozpadají na částice typu $A$ a na začátku jich je $B_0$. Najděte funkci udávající poměr počtů částic typů $A$ a $B$ v čase.
Jáchym vymyslel úlohu do Fyzikálního Náboje, ale nedovolili mu to, prý že by ji nikdo nespočítal. No tak ji dal sem.
(8 bodů)P. složený papír
Každý to jistě někdy slyšel a určitě i zkusil: „List papíru nelze na půlku přeložit více než sedmkrát.“ Je to ale skutečně pravda? Najděte hraniční podmínky.
Kuba se nudil a skládal papír.
(12 bodů)E. magneticky přitažlivá
Společně se zadáním této série jsme vám rozeslali poštou plošný magnet (magnetickou fólii). Tento magnet je trochu jiný než tyčové magnety – v ploše se střídavě střídají severní a jižní pól. Díky tomu se při přiblížení k feromagnetickému povrchu uzavře skrz kov „magnetický obvod“ a magnet drží (např. na ledničce) a unese na sobě třeba i obrázek. Vašimi úkoly jsou:
- Změřit plochu a tloušťku fólie, kterou využijete k experimentům.
- Změřit střední vzdálenost mezi dvěma nejbližšími stejnými magnetickými póly (dvojnásobek opačných).
- Změřit maximální užitečnou hmotnost (tedy hmotnost bez hmotnosti magnetu), kterou unese $1 \mathrm{cm^2}$ magnetu, je-li zatížení magnetu rovnoměrné, pokud magnet přichytíte zespoda k vodorovně umístěnému cca. $1 \mathrm{mm}$ tlustému plechu z magneticky měkké oceli.
Nezapomeňte určit i chyby měření. Fólie, kterou jsme vám dodali, může být samolepící (je přes ni bílá fólie a pod ní lepidlo). V tom případě bílou fólii nahraďte něčím, na co budete upevňovat užitečnou hmotnost.
Karel získal magnetickou fólii.
(10 bodů)S. na procházce s integrály
- Vymyslete tři odlišné příklady markovovského procesu, z toho alespoň jeden fyzikální. Je procházka bez návratu markovovská? A co procházka bez křížení?
- Mějme 2D náhodnou procházku bez návratu na čtvercové síti s počátkem v bodě $(x,y) = (0,0)$, která je omezena absorpčními bariérami $b_1: y = -5$, $b_2: y = 10$. Nalezněte pravděpodobnost, že v bariéře $b_1$ skončíme dříve než v $b_2$.
- Proveďte simulaci pohybu brownovské částice ve 2D a vykreslete graf závislosti střední vzdálenosti od počátku na čase. Uvažujeme diskrétní čas a konstantní délku kroku (jeden krok simulace trvá $\Delta t = \textrm{konst.} $, délka kroku je $\Delta l = \textrm{konst.} $) a umožňujeme pohyb do libovolného směru, tj. každý krok je specifikován délkou a úhlem $\theta \in [0,2\pi )$, přičemž všechny směry jsou stejně pravděpodobné. Zajímá nás především asymptotické chování, tedy vývoj střední vzdálenosti pro $t \gg \Delta t$.
- Chybová funkce je definována vztahem \[ \mathrm{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^x \eu^{-t^2}\,\d t\,.\] Tabelujte tuto funkci, tedy vypočtěte integrál pro mnoho různých $x$. Do řešení nevkládejte tabulku hodnot, ale graf funkce. Zkuste tuto funkci opět numericky zderivovat. Co dostanete?
- Najděte si definici hustoty pravděpodobnosti Maxwellova-Boltzmannova rozdělení $f(v)$, tedy rozdělení rychlostí molekul ideálního plynu. Spočítejte pak pomocí MC integrace střední hodnotu rychlosti definovanou \[ \langle v\rangle = \int_0^{\infty} v f(v)\,\d v\,, \] přičemž pro vzorkování použijte náhodná čísla dle Maxwellova-Boltzmannova rozdělení získaná Metropolisovým-Hastingsovým algoritmem. Hodnotu pro konkrétní zvolené parametry srovnejte s hodnotou z literatury.
Mirek a Lukáš se náhodně procházejí do školy.