1. Série 11. Ročníku

Mějme válec, který je slepený ze dvou skleněných polovin o indexech lomu $n_{1}$ a $n_{2}$. Válec se otáčí rovnoměrně kolem své osy. Na válec svítíme světelným paprskem kolmo na jeho osu rotace (viz obr.). Jak se bude pohybovat stopa paprsku po podložce v závislosti na úhlu natočení $φ$ válce, jestliže je vzdálenost podložky od osy rotace $d=1\,\jd{m}$?

Dva identické zlaté sloupy výšky $200 \,\jd{m}$ a průřezu $1 \,\jd{dm^2}$ jsou umístěny vedle sebe. Jeden z nich je zavěšený a druhý stojí na podložce, oba mají stejnou teplotu $0 \,\C$. Oběma dodáme teplo $5\cdot 10^{6}\, \jd{kJ}$. Budou mít potom stejnou teplotu? Jestliže ne, odhadněte, o kolik se jejich teplota bude lišit. Potřebné údaje si najděte v tabulkách, tepelnou výměnu s okolím zanedbejte.

Slepice se po obědě (12:00) chce dostat do kurníku. Neumí však létat, a jelikož žebřík po stěně kurníku klouže, začne bezradně běhat kolem něj. V kolik hodin se do kurníku dostane, když každou hodinu běhání shodí $40\,\jd{g}$ a ve 14 hodin hodlá snést vajíčko? Ve 12:00 váží slepice $m=1,7\;\mathrm{kg}$, vajíčko má hmotnost $m_{v}=30\,\jd{g}$ a žebřík $M=5\;\mathrm{kg}$. Výška kurníku nad dvorkem je $h=0,85\;\mathrm{m}$, sklon žebříku $α=25°$, součinitel smykového tření mezi kurníkem a žebříkem i mezi dvorkem a žebříkem je stejný: $f=0,7$.

Strýček Skrblík se jednou doslechl o perpetuech mobile a vytušil příležitost, jak ještě více zbohatnout. Vypsal grant na vymýšlení „věčných strojů“, ale jediní, kdo se přihlásili, byli jeho synovci. Přinesli strýčkovi následující tři nápady:

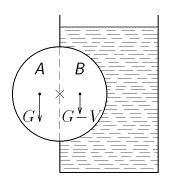
• Základem prvního perpetua je válec, který je dutý, vodotěsný a je upevněn v ose na valivých ložiscích. Obrázek nám objasní funkčnost stroje. Na obě části válce sice působí tíhová síla $G$, ale část $B$ je vůči části $A$ válce nadlehčována vztlakovou silou $V$ dle Archimédova zákona. Válec se bude otáčet a jeho rotační energii převedeme na elektrickou energii.

• Pokud zahřejeme kapalinu, zvětší svůj objem. Zároveň víme, že kapalina je nestlačitelná. Proto budeme kapalinu zahřívat a ochlazovat, změnu jejího objemu převedeme na mechanickou energii a tu na energii elektrickou. Část takto obdržené energie využijeme na zahřívání kapaliny (ochlazení kapaliny zajistí okolní prostředí, odborně „lázeň“). Zbytek energie roztočí stroje ve Skrblíkových továrnách.

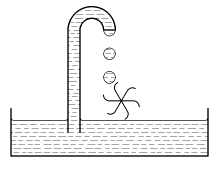
* Do nádoby s vodou je zasunuta kapilára. Díky kapilárním jevům voda naplní celou kapiláru a z horního zahnutého konce odkapává dolů, jak je to vidět na obrázku. Dole je umístěna vodní turbína, která je roztáčena padající vodou, a tak může konat práci.

Strýček se nadšeně pustil do výroby těchto strojů, jaké však bylo jeho zklamání, když zjistil, že ani jediný z nich nefunguje. Od té doby už o žádných „perpetech“ nechce ani slyšet.

Na vás teď je, drazí řešitelé, abyste se pokusili vysvětlit, proč žádný z nápadů synovců strýčka Skrblíka nemůže fungovat jako perpetuum mobile.

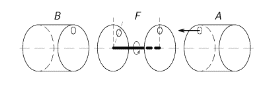
Mějme aparaturu, jejíž schéma je na obrázku. Molekuly opouštějící nádobu s plynem $A$ (teplota $T_{A}$, střední kvadratická rychlost molekul $v_{A})$ tvoří molekulární svazek, jež dále prochází rychlostním filtrem $F$. Pouze částice s rychlostí $v_{F}$ proletí až do nádoby $B$. V prostoru mezi deskami filtru je vakuum, střední volná dráha molekul je větší než rozměr aparatury. Při vhodné volbě rychlosti $v_{F}$ ($v_{F}$ > $v_{A})$ bude teplota nádoby $B$ vyšší než nádoby $A$. Tudíž teplo z tělesa chladnějšího ($A)$ bude přecházet na těleso teplejší ($B)$, což je ve sporu s druhým principem termodynamiky. Vaším úkolem je vysvětlit (ne)správnost této úvahy.

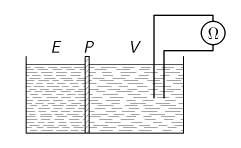
Námětem první experimentální úlohy je jev difúze v kapalině. V kádince je přepážkou $P$ oddělena voda $V$ od roztoku elektrolytu $E$ (např. roztok kuchyňské či jiné soli), viz obrázek. V čase $t_{0}=0 \,\jd{s}$ přepážku odstraníte a ohmmetrem budete sledovat pokles elektrického odporu s časem. Po měření vysvětlete kvalitativně a kvantitativně pozorované změny.

• Určete nejmenší vlnovou délku rentgenového záření rentgenky, v níž jsou elektrony urychlovány napětím $20\,\jd{ kV}$.

• Z jakého kovu byl zhotoven terčík, na nějž dopadaly v rentgence elektrony, pokud spektrální čára $K_{α}$ ve spektru rentgenového záření měla vlnovou délku $(155 ± 3)\cdot 10^{-12}\jd{ m}$?

Návod: Záření rentgenky je dvojího druhu. Pokud elektrickým polem urychlený elektron při dopadu na terčík vyzáří část své kinetické energie v podobě fotonu, vzniká tzv. brzdné záření, jehož spektrum je spojité. Pokud dopadající elektron vyrazí z atomu terčíku elektron z jedné z nejnižších elektronových hladin ($n_{2}$), přeskakuje za malý okamžik na jeho místo nějaký elektron z vyšší hladiny ($n_{1}$), přičemž vyzáří foton o energii odpovídající tomuto přechodu. $K_{α}$ je název spektrální čáry, která vznikne při přeskoku z druhé hladiny ($n_{1}=2$) na první ($n_{2}=1$). V tomto případě však cítí přeskakující elektron efektivní náboj jádra $(Z-1)e$, protože je jádro vůči němu stíněno jedním elektronem, který na nejnižší energetické hladině zbyl.

Literatura: Arthur Beiser: Úvod do moderní fyziky, Academia, Praha 1978.