6. Série 11. Ročníku
Termín uploadu: -
1. síť sítí
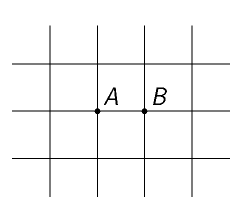
Spočtěte elektrický odpor $R$ mezi body $A$ a $B$ nekonečně rozlehlé čtvercové sítě (viz obr. 1). Jednotlivé úsečky tvořící síť mají odpor $R_{0}$.
2. izotop
Na pracoviště nukleární medicíny byla doručena zásilka izotopu A. V dokumentech, které přišly spolu s izotopem, bylo uvedeno, že 11,5 min po vyndání z reaktoru, kde tento izotop vzniká v čisté formě, byla aktivita zásilky 1000 rozpadů gamma za sekundu. Když přeměřil aktivitu doručené zásilky bezpečnostní technik, zjistil, že je také 1000 rozpadů gamma za sekundu. Určete dobu transportu zásilky, když víte, že se A rozpadá beta rozpadem s poločasem 23 minut na B, které se s poločasem 23 dní rozpadá za emise beta a gamma na stabilní nuklid C.
3. kostka
Když se pokusíme uchopit kostku tak, jak je naznačeno na obrázku, ne vždy se nám to povede. Určete podmínku, za které se to podaří.
4. alternátor
Představte si rotující kovový disk (disk rotuje kolem pevné osy identické s osou rotační symetrie disku) v časově neměnném magnetickém poli tak, že vektor $\textbf{B}$ magnetické indukce pole směřuje kolmo na plochu disku. Určete napětí (měřené naprázdno) mezi kterýmikoli dvěma body disku, případně i proud, který by tekl měřícím obvodem, kdyby měřící přístroj neměl ideálně nekonečný odpor.
P. zastavení v zatáčce
Představte si, že jednou budou u nás vlaky jezdit opravdu rychle. Nechť rychlík zastaví v oblouku o poloměru $500\,\jd{ m}$, který je klopen pro rychlost $200\,\jd {km/h}$ (tzn. že na cestující v jedoucím rychlíku působí neustále síla jen kolmo dolů). A protože lidé jsou zvědaví, vykloní se všichni z oken na vnitřní straně oblouku, aby zjistili, co se děje. Vaším úkolem je zjistit, kolik lidí musí ve vlaku být, aby se překlopil.
Vlak je složen z 10 čtyřosých rychlíkových vozů o délce $25\,\jd{ m}$, šířce $3\,\jd{ m}$, výšce $4,2\,\jd{ m}$ a hmotnosti $40\,\jd{ t}$. Těžiště vozu je ve výšce $1,2\,\jd{ m }$ od hlavy kolejnice, rozchod koleji je $1738\,\jd{ mm}$. Spodní okraj otevřeného okna nechť je ve výšce $2,5\,\jd{ m}$.
E. akvárium
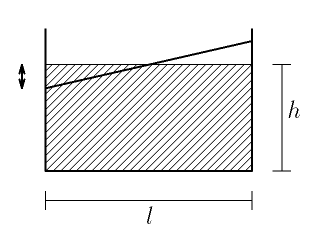
Najděte si akvárium, nebo podobnou nepropustnou nádobu kvádrového tvaru a zčásti ji naplňte vodou do výšky $h$. Nádobou rychle pohněte ve směru jedné ze stěn, aby hladina začala kmitat tak, jak je to naznačeno na obrázku. Změřte frekvenci, s kterou hladina kmitá, proveďte pokud možno více měření pro různé hodnoty $h$ a $l$ a výsledky se pokuste interpretovat (vymyslete fyzikální model). Omezte se na malé amplitudy kmitů.
S. hmotnost pionu a zákony zachování
Najděte horní řádový odhad hmotnosti mezonu $π^{0}$, který podle Yukawovy teorie zprostředkovává silnou interakci mezi dvěma neutrony, když víte, že její dosah je zhruba $10^{-15}\,\jd{ m}$. Vzpomeňte si na „relaci neurčitosti mezi časem a energií“, uvažte, že energie, která se nezachovává je minimálně $m_{π}c^{2}$, a že pion za příslušný čas nemůže doletět dál než světlo ve vakuu.
Rozhodněte, zda mohou podle současných znalostí v principu proběhnout následující procesy
$$p^{+} + e^{-} → K^{-} + e^{+} + ν_{e} + ν_{e}\,,$$
$$π^{0} + μ^{+} → e^{+} + ν_{μ} + ν_{e}\,,$$
$$Δ^{++} → p^{+} + π^{0}\,,$$
a svůj výsledek zdůvodněte.