1. Série 27. Ročníku
Termín uploadu: -
(2 body)1. zlatá přehrada
Kolik cihliček (kvádříků) ze čtyřiadvaceti karátového zlata o rozměrech $10\;\mathrm{cm}$, $3 \;\mathrm{cm}$ a $1 \;\mathrm{cm}$ by se vešlo do vodní nádrže Orlík? Jaký zhruba tlak bude působit na cihličku, která je na dně v nejhlubším místě nádrže?
Karel se chtěl topit ve zlatě.
(2 body)2. nezastavitelný terminátor
Jak rychle se pohybuje hranice světla a tmy (terminátor) na povrchu Měsíce? Je možné utíkat před tmou, když jste na rovníku?
Karel se už zase díval na Futuramu
(4 body)3. bublina v ropovodu
Máme malou kulatou bublinku plynu v kapalině, která teče nějakou rychlostí vodorovným potrubím. Jak se změní její rozměry, když se dostane do místa, kde je potrubí zúžené? K čemu se to dá využít, nebo naopak kde to dělá problémy? Uvažujte laminární proudění.
Karel se zamyslel nad osvěžovačem vzduchu.
(4 body)4. kostka v bazénu
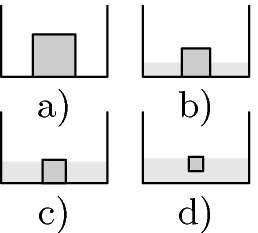
Na dně prázdného bazénu s dnem plochy $S$ leží ledová kostka (z vody) o hraně délky $a$. Kostka se rozpouští ze všech stran stejnoměrně tak, že si je stále podobná. Jaká její část se rozpustí, než začne plovat?
Lukáš koukal na zamrzlou Bílinu.
(5 bodů)5. korálek

Bodový korálek o hmotnosti $m$ a s nábojem $q$ se pohybuje v rovné trubce bez tření. Trubka se nachází ve středu mezi dvěma nabitými koulemi, každá s nábojem $Q=-q$. Vzdálenost koulí je 2$a$. Uvažujte elektrostatické působení a najděte frekvenci malých kmitů korálku okolo rovnovážné polohy.
Nápověda: Uvědomte si, že velikost síly se při malých výchylkách mění pouze zanedbatelně.
Radomír se kutálel v trubce.
(5 bodů)P. rychlost světa
Jaký by byl svět, ve kterém by byly stejné hodnoty fundamentálních fyzikálních konstant, jenom rychlost světla by byla pouze $c=1000\;\mathrm{km}\cdot \mathrm{h^{-1}}$? Jaký by byl takový svět pro život na Zemi, život lidí? A bylo by vůbec možné, aby v takovém světě existovali lidé?
Karel zase navrhl neřešitelnou úlohu.
(8 bodů)E. Ohni to, neohýbej to!
Vaším úkolem je změřit vzdálenosti vrypů na difrakční fólii pomocí světla ze třech různobarevných LED-diod. V případě zájmu si neváhejte o potřebné věci napsat na email experiment@fykos.cz a my vám obratem poštou zašleme tři LED-diody, odpor, vodiče a samozřejmě i difrakční fólii. Jediné, co si budete muset dokoupit, je baterie o napětí $9\;\mathrm{V}$. Poznámka: Zaslané věci nevyhazujte, možná se budou ještě hodit.
Karel rozfofroval rozpočet.
(6 bodů)S. relativistická
- Kvantovou gravitaci potřebujeme jen při studiu velmi malých vzdáleností, kdy jsou gravitační síla a kvantové efekty rovnocenné. Gravitační sílu charakterizuje gravitační konstanta, kvantovou mechaniku Planckova konstanta a speciální teorii relativity rychlost světla. Najděte hodnoty těchto konstant v tabulkách a zkuste z nich vzájemným násobením a umocňováním získat veličinu s jednotkou délky. Tak získáte délkovou škálu, na které je relevantní gravitace a kvantová mechanika současně.
- Ukažte, že provedeme-li speciální Lorentzovu transformaci (tj. přejdeme do systém pohybujícímu se vůči původnímu rychlostí $v$ ve směru osy $x^1$)
$$x^0_\mathrm{nov}=\frac{x^0-\frac{v}{c}x^1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}\,,\quad x^1_\mathrm{nov}=\frac{-\frac{v}{c}x^0+ x^1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}\,,\quad x^2_\mathrm{nov}= x^2\,,\quad x^3_\mathrm{nov}= x^3 \, ,$$ potom se hodnota čtyřintervalu nezmění.
- Vzpomeňte na definici čtyřintervalu a položte $Δx^3 = Δx^2 = 0$. Máme pak $$(\Delta s)^2 = -\(\Delta x^0\)^2+ \(\Delta x^1\)^2\,.$$
V jaké části roviny $(Δx^{0},Δx^1)$ je čtyřinterval $(Δs)^2$ záporný a kde kladný? Jak vypadá křivka definovaná ( $Δs)=0?$