2. Série 1. Ročníku
Termín uploadu: -
1. silák
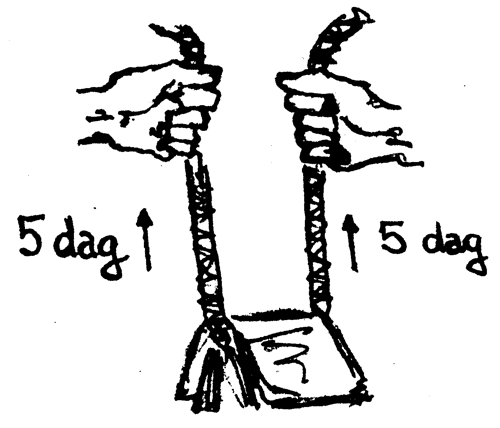
Uvolněné lano

Vodorovně napnuté lano
Za devatero horami je země, v níž se síla měří v jednotkách zvaných $\textrm{dag}$. Na pouti tam silák napíná oběma rukama lano, na němž je zavěšen telefonní seznam o tíze $10\; \textrm{dagů}$. (Kdyby silák držel oba konce provazu u sebe, napětí v obou částech lana by bylo $5\; \textrm{dagů}$.) Jaké bude napětí v obou částech lana, když silák roztáhne lano do vodorovné polohy?
- $5\; \textrm{dagů}$
- $10\; \textrm{dagů}$
- $20\; \textrm{dagů}$
- více než milión $\textrm{dagů}$
2. čluny

Pohled na čluny
Obrázek ukazuje dva čluny pohybující se po hladině jezera. Z obálky vln soudíme, že
- obě lodi plují větší rychlostí, než je rychlost povrchových vln, přičemž loď I pluje rychleji než loď II
- loď I pluje rychleji než loď II, ale nemusí nutně plout větší rychlostí, než je rychlost povrchových vln
- ani a), ani b)
3. Křemílek

Miska s Křemílkem a kuličkou
Křemílek chce dostat z misky těžkou kuličku. Stěny misky jsou však příliš strmé, aby ji vykulil přímo. Svými silami
- může dostat kuličku ven. (Jak?)
- nemůže dostat kuličku ven.
4. pružiny
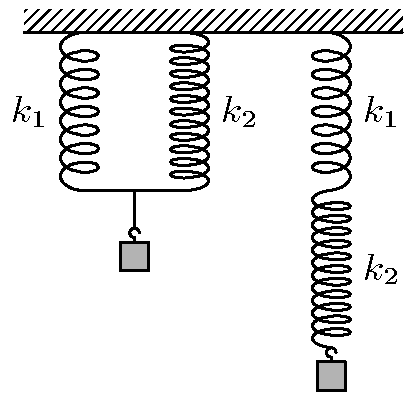
Model pružin
Pohrajme si s dvěma stejně dlouhými, ale různě tuhými pružinami. (Jejich tuhosti označíme $k_{1}$ a $k_{2}$.) Když je spojíme (viz obrázek), chovají se dohromady jako jediná pružina? Jaká je tuhost $k_{výsl}$ této „výsledné“ pružiny při spojení vedle sebe a jaká při spojení za sebou?
P. balónek
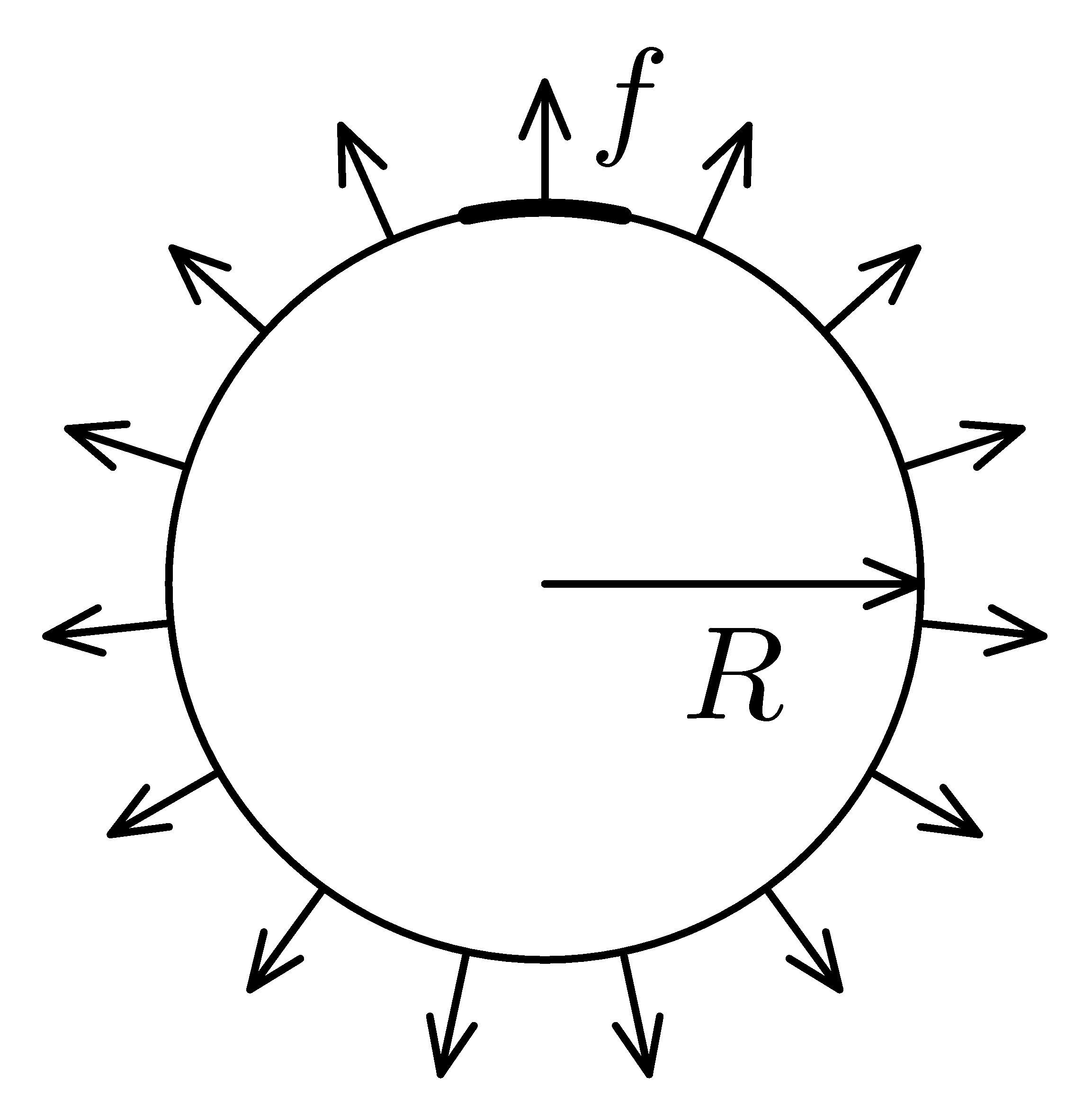
Model balónku
Jak moc můžete nafouknout pouťový balónek, než praskne? Předpokládejme, že balónek má tvar koule. V nenafouknutém (nebo velmi slabě nafouknutém) stavu nechť má poloměr $r_{0}$ (třeba $5\; \textrm{cm}$). Je z gumové blány, jejíž elastické vlastnosti i pevnost známe. Na obrázku je znázorněn kruh vystřižený z materiálu, z něhož je balónek. Tučně vyznačená délka obvodu je jednotková. Pro jednoduchost předpokládejme, že kdybychom kruh z této blány roztahovali na okraji (viz obrázek) tak, že by síla na jednotku délky obvodu kruhu byla $f$, byl by poloměr kruhu přímo úměrný $f$.
$R=R_{0}(1+αf)$. Maximální síla na jednotku délky (při níž materiál balónku praskne) nechť je $f_{max}$.
Předpokládejme dále, že na jedno nadechnutí naberete do plic objem $V_{fuk}$ vzduchu a ten pak fouknete do balónku. Kolikrát můžete do balónku fouknout, než praskne, a jaký bude mít rozměr? (Zkuste též odhadnout reálné hodnoty veličin v problému vystupujících a diskutovat oprávněnost předpokladů.)
E. domino
K této úloze budete potřebovat kostičky domina. Postavte si řadu těchto kostiček za sebou. Ťuknete-li lehce do krajní kostičky, začne padat, porazí druhou, ta třetí… Vidíme, že řadou kostiček bude probíhat „vlna“. Experimentujte s touto soustavou.
Změřte rychlost šíření této vlny v závislosti na vzdálenosti kostiček. Zkuste měnit další podmínky vašeho experimentu (např. nakloňte rovinu, na níž kostičky stojí, změňte materiál podložky – hladký, drsný – atd.). Není-li pro vás dostupné domino, zkuste použít třeba krabičky od sirek či jiné vhodné objekty.
Snažte se výsledky fyzikálně komentovat, eventuelně i teoreticky vysvětlit.
S. odpor působící na auto
Spočtěte, jak bude s časem klesat rychlost auta brzděného jen odporem vzduchu. Auto jede po rovině na neutrál a zanedbáme valivé tření kol atd. – vše kromě odporu vzduchu.
Návod: Síla, kterou je auto brzděno, je v daném případě zhruba úměrná druhé mocnině jeho rychlosti: $F_{brzd}=C\cdot v$. (Pro běžný automobil lze odhadnout $C=(1–2)\; \textrm{m}^{-2}\cdot \textrm{s}$.) Uvažte, že během krátkého časového intervalu $Δt$ se síla působící na automobil příliš nezmění a jeho pohyb tedy můžeme brát jako rovnoměrně zpomalený. Celkovou změnu rychlosti za delší čas dostaneme poskládáním změn v jednotlivých „kouscích“ $Δt$.
Problém tak lze velmi dobře simulovat na mikropočítači, ale můžete využít i obyčejnou kalkulačku a hodnoty psát na papír, vynášet do grafu apod. Úlohu si můžete i rozšířit a počítat též ujetou dráhu, případně uvažovat změněné podmínky: jízdu z kopce či do kopce, jízdu pod vodou ($Cρ_{prostředí}$), vynalézavosti se meze nekladou.