2. Série 26. Ročníku

Centra měst Drážďan a Vídně jsou od sebe vzdálena zhruba $d=370\;\mathrm{km}$ vzdušnou čarou po Zemi. O co kratší by byla vzdálenost mezi nimi, pokud bychom mohli jít přímým tunelem skrz Zemi? Zanedbejte rozdíl nadmořských výšek, ve kterých jsou města položena. Na závěr můžete srovnat i délku cesty, kterou byste mezi městy jeli autem. Aby byla tato úloha jednoduchá, je zde nápověda. Goniometrické funkce můžeme pro malé úhly aproximovat (tedy přiblížit) jako $$ \mathrm{sin} α ≈ α - α^{3}/6 \,,\\ \mathrm{cos} α ≈ 1 - α^{2}/2 \,,\\ \mathrm{tg} α ≈ α + α^{3}/3 \,, $$ kde úhel dosazujeme v radiánech. Toho můžeme využít pro vyjádření neznámé v rovnici, kde vystupuje jak samotný úhel, tak i obsažený v nějaké goniometrické funkci.

Kdyby se všechna hmota Země vzala a přemodelovala se na kulovou slupku o tloušťce $d=1\;\mathrm{km}$ (se stejnou hustotou), jaký by tato nová „Země“ měla vnější poloměr? Jaké by bylo gravitační zrychlení na jejím vnějším povrchu?

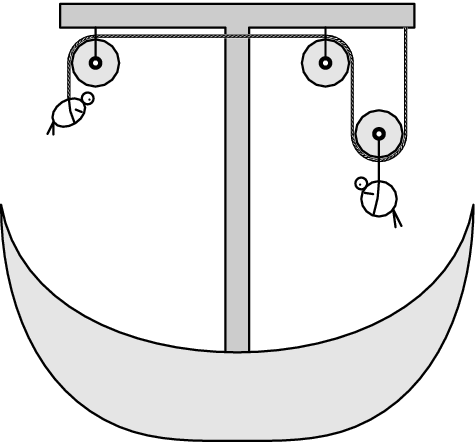
Dva mladí, ale bohužel poněkud prostorově výraznější, Benátčané Paolo a Francesca Muschetti (o hmotnostech $m_{P}=180\;\mathrm{kg}$ a $m_{F}=130\;\mathrm{kg}$) by se chtěli spolu projet na gondole. Žádný gondoliér je ale nechce vzít na svou loď, protože ví, že by je všechny tři loď neunesla. Chytrý gondoliér Jacopo ale vymyslel rampu, na kterou umístil tři kladky dle obrázku. Skrz kladky provlékl lano a oba mladé Benátčany na ně upevnil, viz obrázek – každého na opačný konec, tak, že nejprve byla nahoře lehčí Francesca a po jisté chvíli ji v této pozici vystřídal těžší Paolo. Jak vysoká musí být rampa, aby gondola stihla přejet přes kanál? Doba jízdy je $τ=60\;\mathrm{s}$. Přepokládejme, že při použití tohoto zařízení se již gondola nepotopí. Zanedbejte veškeré tření, hmotnost lana a momenty setrvačnosti kladek.

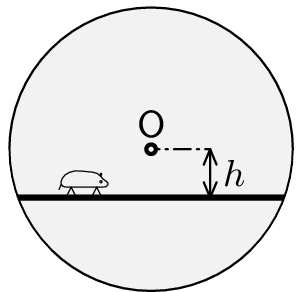
Rado si pro svého křečka Bobka přichystal speciální kolečko. Celá soustava se může otáčet okolo osy procházející bodem $O$, který je středem kolečka, a ke kolečku je vodorovně připojená deska ve vzdálenosti $h$ od osy rotace, viz obrázek. Jak se má křeček Bobek pohybovat po desce, aby deska zůstala po celou dobu pohybu vodorovně? Koeficient tření mezi křečkem a deskou je $f$.

V U-trubici je rtuť se vzduchovou bublinou výšky $h_{0}$ v jednom rameni, jak můžete vidět na obrázku. Co se stane, pokud se okolní atmosféra změní následujícími způsoby? Předpokládejte, že rtuť při změně teploty nemění objem (hustotu), stejně tak i sklo, ze kterého je U-trubice, a vzduch se chová jako ideální plyn. Původní stav okolní atmosféry je popsán teplotou $T_{0}=300K$, tlakem $p_{a}=10\cdot 10^{5}Pa$ a složením je vzduch. Předpokládejte, že celý systém je stále v termodynamické rovnováze, rovněž bublinu považujte za válec.

• Okolní teplota se zvýší na dvojnásobek a přitom budou ramena U-trubice volná.
• Okolní teplota se zvýší na dvojnásobek, ale před touto změnou pevně uzavřeme oba konce U-trubice.
• Okolní teplota se zvýší na dvojnásobek, ale před zahřátím pevně uzavřeme pouze jeden konec U-trubice. Pro všechny body zadání určete výsledné rozměry bubliny ve rtuti a výškový rozdíl mezi hladinami v obou částech U-trubice.

Bonus: Započtěte lineární teplotní roztažnost rtuti.

Co kdyby se „přes noc“ změnila hodnota gravitační konstanty na dvojnásobek a přitom by zůstaly zachovány ostatní fyzikální konstanty na původních hodnotách? A co kdyby se zvětšila stokrát? Rozepište se o různých aspektech – zejména o životě na Zemi a drahách vesmírných objektů.

Určete průměrnou plochu listu vámi vybraného stromu (či keře). Nezapomeňte na statistické zpracování vašich dat. Odhadněte, kolik energie ze slunečního záření může váš strom použít pomocí chlorofylu na tvorbu cukrů za jeden den, rok.

• Které drifty budeme pozorovat v lineární pasti? Představte si, že je osa pasti vodorovná, bude v pohybu částic hrat významnou roli drift způsobený gravitační silou?

• Odvoďte vztah pro ztrátový kužel a nakreslete originální obrázek, který bude názorně ilustrovat chování částic v lineární pasti.

• Odvoďte vztah pro drift způsobený elektrickým polem, které je kolmé na magnetické pole a má konstantní gradient ve směru svého působení. Diskutujte různé typy pohybu částice v závislosti na velikosti gradientu.