4. Série 18. Ročníku

Sovětským generálům došla trpělivost. Už se nemohli dívat na provokace ze strany amerických imperialistů a stiskli červený knoflík na odpálení atomové bomby. Hned nato do řídicí místnosti přiběhl mladý poručík, který byl zodpovědný za propočítání dráhy letu, že si prý při výpočtech trochu přihnul ze stakanu vodky a důsledkem toho místo na New York míří raketa na spřátelenou Kubu.

Naštěstí je ale po ruce náhradní bomba, kterou by se ta původní dala sestřelit, čímž by se zamezilo rozkolu v socialistickém táboře. Původní raketa byla vystřelena rychlostí $v$ pod úhlem $α$. Jak mají sovětští experti nastavit úhel odpálení $β$ druhé rakety, aby tu první zasáhli, když mezi oběma odpaly je časová prodleva $T?$

Diskutujte, kdy se dá mír mezi spřátelenými zeměmi zachránit a kdy už ne. Odpor vzduchu zanedbejte. Všichni samozřejmě víte, že Země je placatá a její gravitační pole je homogenní.

Váleček o malém poloměru $r$ a hmotnosti $m$ se kutálí z nakloněné roviny a na jejím konci přejde hladce do vodorovného pohybu po podložce. Přitom na sebe namotává nit o délkové hustotě $ρ$. V jaké vzdálenosti od konce nakloněné roviny se váleček zastaví? Dále znáte výšku nakloněné roviny $h$ a její sklon $α$. Tření zanedbávejte.

Jeden z vítězů Superstar narazil na problém. Jeho nová limuzína je příliš dlouhá na to, aby se vešla do jeho staré garáže. Jeho kamarád, který studuje fyziku, si však věděl rady. Jelikož dobře zná práci Alberta Einsteina, uvědomil si, že pokud se limuzína rozjede dostatečně rychle, zkrátí se její délka z pohledu stojícího pozorovatele natolik, že se již do garáže vejde.

Na začátku a na konci garáže jsou umístěny padací dveře, které se spustí ve chvíli, kdy celá limuzína bude uvnitř. Z pohledu superstar v limuzíně se však naopak v důsledku kontrakce délek zkrátí garáž a vůz se do ní určitě nevejde. Rozhodněte, zda je možné tímto způsobem limuzínu do této garáže zaparkovat.

Frekvence fotonu vyzářeného jádrem radioaktivního železa není vždy stejná, ale při rozpadech různých jader se nepatrně liší (to platí i pro jiná jádra). Pro jednoduchost předpokládejte, že hodnota energie fotonu v klidové soustavě jádra železa leží náhodně v intervalu ( $E_{0}-ΔE,E_{0}+ΔE)$, kde $E_{0}=14,4\;\mathrm{keV}$ (keV = kiloelektronvolt), $ΔE≈10^{-8}\;\mathrm{eV}$ ($1\, \jd{eV} = 1,602 \cdot 10^{-19} \jd{J}$).

• Vyzáří-li volný nehybný atom železa foton, musí mít tento atom podle zákona zachování hybnosti opačnou hybnost než vyzářený foton. Vypočítejte kinetickou energii takového atomu a porovnejte ji s veličinou $ΔE$.
• Takzvaný Mössbauerův jev spočívá v tom, že je-li foton vyzářen atomem železa vázaným v krystalu, může se hybnost „zpětného rázu“ předat celému krystalu. Vypočítejte kinetickou energii krystalu (posun energie fotonu) v tomto případě za předpokladu, že krystal je složen z řádově $10^{23}$ atomů.

Stejně jako emise fotonu může probíhat i jeho absorpce. Foton však může být absorbován jen tehdy, když jeho energie v klidové soustavě jádra leží v intervalu ( $E_{0}-ΔE,E_{0}+ΔE)$.

• Rozhodněte, zda může nehybný atom železa absorbovat foton vyzářený jiným nehybným atomem.
• Vypočítejte, jak rychle se vůči sobě musí pohybovat dva kusy železa, aby už první kus nemohl kvůli Dopplerovu jevu absorbovat fotony vyzářené druhým kusem. Dopplerovým jevem myslíme to, že frekvence záření $f$, kterou vyzařuje zdroj přibližující se rychlostí $v$, se v naší soustavě změní na $f′=(1+v⁄c)f$.

Předpokládejte, že při emisi i absorpci se uplatňuje výše zmíněný Mössbauerův jev.

Potřebné konstanty nalezněte v tabulkách.

Kroužením mokrým prstem po hraně broušené skleničky (například na víno) lze vyloudit poměrně intenzivní zvuk. Pokud se do skleničky nalije voda, pak frekvence vyluzovaného tónu klesá se vzrůstající výškou hladiny. Sami si to vyzkoušejte a pokuste se tento jev vysvětlit.

Organizátoři FYKOSu popíjeli v menze po večeři výborný čaj. Protože jsou to zvídaví lidé, zamysleli se někteří z nich nad procesem chladnutí čaje. Předmětem sporu bylo, do jaké míry přispívají k chladnutí čaje procesy vypařování, vedení tepla a vyzařování. Pokuste se stejný problém řešit experimentálně.

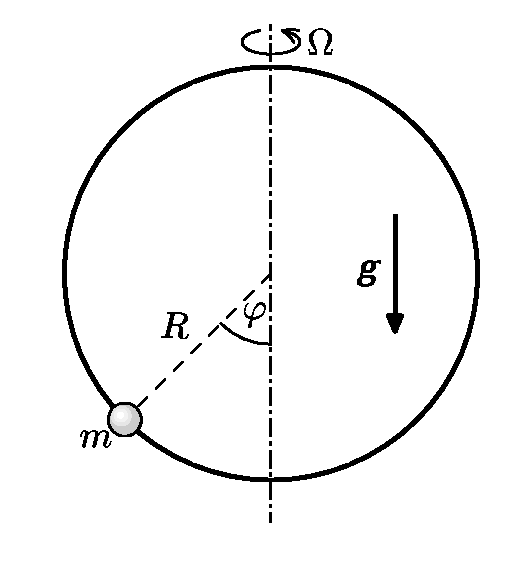
Malý korálek o hmotnosti $m$ klouže bez tření na drátu ve tvaru kruhové smyčky poloměru $R$, smyčka se otáčí konstantní úhlovou rychlostí $Ω$ kolem svislé osy (viz obrázek).

• Vhodně zvolte zobecněnou souřadnici a sestrojte Lagrangeovu funkci problému.
• Sestavte Lagrangeovu rovnici 2. druhu, která popisuje pohyb korálku.
• Rozhodněte, kdy je rovnovážná poloha v nejnižší poloze smyčky stabilní a kdy je labilní v závislosti na $Ω$. Pro $Ω$, kdy je tato poloha stabilní, vypočítejte periodu kmitů korálku kolem této polohy.
• Za bonusové body nalezněte další rovnovážné polohy a diskutujte, zda jsou stabilní, nebo labilní. Pokud jsou stabilní, určete periodu kmitů kuličky kolem těchto rovnovážných poloh.