4. Série 19. Ročníku

Kdesi v dalekém vesmíru za 1001 hvězdami a jednou černou dírou byla nebyla planeta Balónků. Tyto inteligentní duté bytosti každý rok pořádají soutěž „Čím výš, tím líp“.

Každý z balónků si přiváže provázek, aby bylo možné určit jeho výšku. Aby se mohli Balónci účastnit soutěže, musí mít všichni stejné parametry. Kupodivu nikdo zatím nikdy nevyhrál. Délková hustota provázku je 11 luftíků na špurgl, hustota atmosféry je 110101 luftíků na krychlový špurgl, poloměr každého z balónků je 10 špurglů, hmotnost Balónka je 10 luftíků. Při pádu tělesa v tíhovém poli na planetě Balónků se za každý temp jeho rychlost zvýší o 111 špurglů za temp. Určete, jakou maximální výšku Balónka hlavní rozhodčí soutěže naměří a jak se bude Balónek pohybovat po dosažení této výšky. Nezvednutá část provázku každého Balónka leží volně na zemi. Závody Balónků probíhají v malých výškách, kde je hustota atmosféry přibližně konstantní.

Nápověda: Každý balónek má maximálně jeden provázek.

NASA chystá velkou výpravu na planetu Balónků za účelem navázání komunikace s tamními inteligentními dutými bytostmi. Špiónům se podařilo zjistit od místních informátorů následující údaje: atmosféra je složena z plynu o muškové hmotnosti 10001 luftíků na mušku, počet molekul atmosféry v jedné mušce je $10^{1101}$, tloušťka atmosféry je $10^{10001}$ špurglů a srovnáním teploměrů obou civilizací špióni určili, že sedmi pozemským kelvinů odpovídá jeden luftík krát špurgl čtverečný na temp čtverečný.

Určete teplotu na povrchu planety a rozhodněte, zda by si měli kosmonauti vzít spíše tričko či kožich. Při řešení se vám můžou hodit i údaje z již zmíněné soutěže.

V hlavním městě planety Balónků Medicinbaldorfu se jednou za debrecinský megatemp koná pouť. Hlavní atrakcí je speciální balónkovský kolotoč, který se Funík s Pískalem rozhodli navštívit.

Dutou tyčí délky $L$ je provlečen provázek délky $l>L$. Na jeden konec provázku se přivázal Funík, na druhý konec Pískal. Oba kamarádi by měli vážit stejně, Funík ale ke snídani snědl kousek rozemleté traverzy a je o trošku těžší. Poté se tyč začne točit kolem svislé osy na ní kolmé. Určete polohu osy tak, aby vodorovná vzdálenost mezi Balónky byla co největší.

… a už zní svatební síní slavnostní pískot a fukot. Ano, je to tak, Pískal s Foukalkou si dnes řeknou své písk. A už je tu první novomanželský polibek, při němž se spojí svými otvory. Poté kněz slavnostně rozváže provázky a dojde k propojení. Popište, co bude následovat. Nezapomeňte, že všichni svobodní Balónci mají stejné parametry.

Na planetě Balónků došlo k revoluci a k moci se dostali fundamentalisté, kteří zakázali jíst traverzy se šlehačkou. Jelikož šlo o Funíkovo oblíbené jídlo, nezbylo mu nic jiného, než odejít do dobrovolné emigrace.

Při příletu na Zem byl Funík zavřen do karantény a byl mu změřen objem $V$ a teplota $T$. Imigrační úřad však rozhodl, že nedostane azyl, pokud nezmění svůj objem na $V′$ a teplotu na $T′$. Funík nemůže v karanténě přijímat ani odevzdávat žádné teplo, měnit počet částic, ze kterých je složen, i na traverzy se šlehačkou si prozatím musí nechat zajít chuť. Poraďte Funíkovi, jak to má udělat, aby mohl na Zemi prožít šťastný a spokojený život.

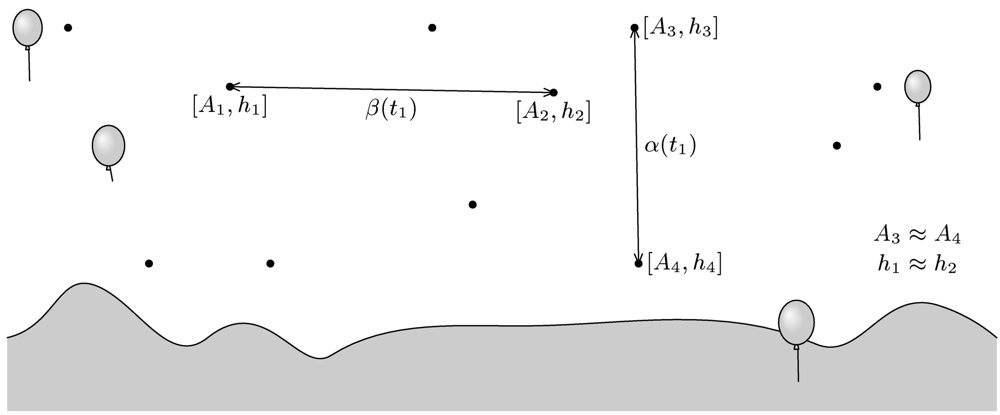
Balónci při pozorování oblohy často soudí, že se jim souhvězdí vysoko nad hlavou zdají menší, než když si je prohlížejí nízko nad obzorem. Proveďte pozorování na Zemi a měřením ověřte, zda jde skutečně o klam. Změřte úhlovou vzdálenost $α(t_{1})$ dvou vybraných hvězd, které jsou přibližně nad sebou (mají stejný azimut $A)$, a úhlovou vzdálenost $β(t_{1})$ jiných dvou hvězd, které jsou ve stejné výšce $h$ nad obzorem, (tzn. kontrola v obou nezávislých směrech) v okamžiku, kdy se tyto hvězdy nacházejí $co$ nejníže nad obzorem. Až později stejné dvojice hvězd najdete v co největší výšce, měření obou úhlových vzdáleností $α(t_{2})$, $β(t_{2})$ zopakujte. Snažte se pochopitelně měřit co nejpřesněji!

Zvlášť oceníme, pokud ze znalosti katalogizovaných souřadnic hvězd přesně vypočítáte jejich teoretickou úhlovou vzdálenost. Nezapomeňte popsat použité pomůcky a zamyslet se nad jejich výhodami a nevýhodami (resp. diskutovat přesnost měření), uvést důležité podmínky měření a určit zkoumané hvězdy – alespoň načrtněte mapku hvězdného okolí a uveďte směr (např. jih) a čas měření. Vyhodnoťte chyby měření a v diskusi srovnejte výsledky.

1. Jakou tepelnou kapacitu plynu složeného z tříatomových molekul s atomy uspořádanými do vrcholů trojúhelníku předpovídá klasická fyzika? Na jakou hodnotu tato kapacita poklesne při snížení teploty na 100 K?
2. Zjistěte chování výrazů pro vnitřní energii krystalu a energetické spektrum záření černého tělesa pro malé teploty. Odvoďte dále tzv. Wienův posunovací zákon. Ten říká, že frekvence $ω_{m}$, pro níž má závislost intenzity záření černého tělesa na teplotě maximum, je přímo úměrná teplotě.
3. Vypracujte lepší teorii tepelné kapacity krystalu, aby uvažovala kolektivní kmity atomů. Případné integrály nemusíte počítat.

Nápověda: Uvědomte si, že se krystalem šíří zvukové vlny (jak příčné, tak podélné, a to různými rychlostmi). Počet módů nemůže být větší, než je počet stupňů volnosti $3N$ krystalu ($N$ je počet částic).