5. Série 25. Ročníku

Hodíme-li do sklenice s vodou šumivý prášek, tak nejprve leží na dně a potom se zvedne. Proč?

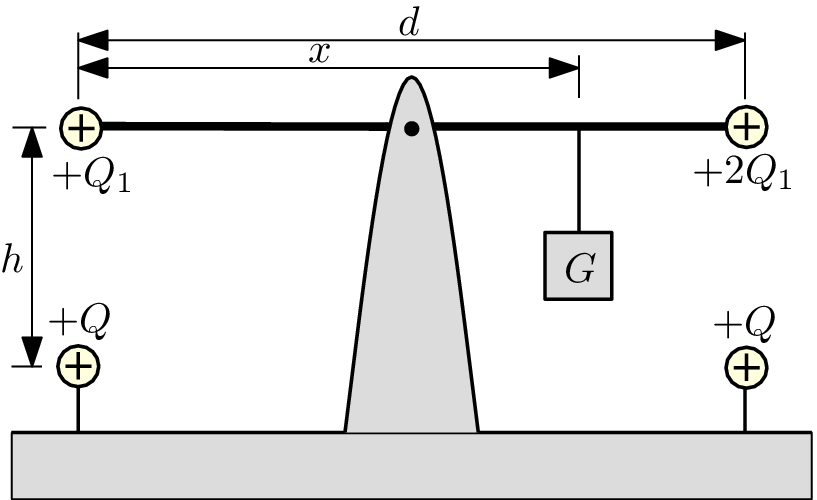
Na obrázku je nevodivá tyč délky $d$ zanedbatelné hmotnosti, otočná kolem svého středu. Na obou koncích tyče jsou připevněny malé vodivé koule zanedbatelných hmotností s kladnými náboji $Q_{1}$ a 2$Q_{1}$. Tyč je vyvážena závažím o tíze $G$ podle obrázku. Ve vzdálenosti $h$ přímo pod každou z koulí je pevně umístěna koule s kladným nábojem $Q$.

• Určete vzdálenost $x$, pro niž je tyč vodorovná a je v rovnováze.
• Pro jakou hodnotu $h$ bude tyč v rovnováze a nebude přitom vůbec zatěžovat čep, na němž je upevněna?

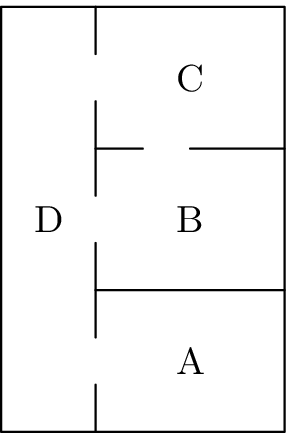
Aleš bydlí ve čtyřpokojovém bytě, jehož půdorys si můžete prohlédnout na obrázku. Mára se ale rozhodl, že Alešův byt zamoří nepříjemnými mravenci faraony. Faraoni po bytu šíleně rychle pobíhají a to ještě navíc šíleným způsobem – můžete uvažovat, že jednou za pět minut se 60$%$ mravenců přesune do sousedních místností a jenom 40$%$ jich zůstává pobíhat ve stejné místnosti, co předtím. Přitom se rovnoměrně rozbíhají do sousedních místností (když má místnost dvoje dveře, tak 30$%$ jich přeběhne do jedné a 30$%$ do druhé, když má troje dveře, tak se rozdělí po 20$%)$. A to se opakuje každých pět minut (uvažujte jenom kroky přesně po pěti minutách). Faraonům se v bytě líbí a tak neutíkají ven. Na druhou stranu se faraoni nemají šanci jinak dostat do bytu než propašováním a to dělá jenom Mára, takže jinak ani faraoni v bytu nepřibývají.

• Když Mára zlomyslně umístí 1000 faraonů do předsíně (D), kolik faraonů bude v jednotlivých místnostech po pěti minutách? Kolik jich bude po deseti minutách a po patnácti minutách? (2 body)

• Pokud jsme našli v místnostech počty mravenců $N_{A}=12$, $N_{B}=25$, $N_{C}=25$ a $N_{D}=37$, jak byli mravenci rozmístění před pěti minutami? (1 bod)

• Bonus: Kolik mravenců by bylo v místnostech po hodně dlouhé (prakticky nekonečné) době, když by Mára rozmístil faraony jako v bodu a)? Závisí to na tom, jak Mára mravence rozmístil? A nejrafinovanější otázka - ustálí se počet mravenců na jedné hodnotě, nebo bude oscilovat? (bod/y navíc)

Maminka má kočárek o hmotnosti $m$ a je s ním pevně spojena vláknem délky $l$, které je na počátku natažené. Mezi maminkou i kočárkem a podlahou, na které oba stojí, je nenulový koeficient smykového tření $f$. Maminka začne kočárek táhnout po přímce konstantní rychlostí $v$, která je kolmá na počáteční polohu vlákna. Popište trajektorii kočárku v závislosti na parametrech úlohy. Maminku i kočárek považujte za hmotné body. Doporučujeme úlohu numericky simulovat.

O kolik musíme zvýšit výkon motoru na jednoho chyceného ptáka za sekundu, pokud nad vagonem vztyčíme síť, do níž chytáme nebohé ptáky? Vlak jede rychlostí $v$, pták váží $m$, jeho rychlost je $w$, úhel nalétnutí do sítě je $φ$ a síť má plochu $S$. Předpokládejte, že mezi jednotlivými záchyty se síť vrátí vždy do klidové polohy.

Navrhněte konstrukci světelného meče, aby byl sestrojitelný za současného poznání vědy a techniky a přitom vypadal i fungoval podobně, jako ten autentický ze Star Wars.

V obálce vám spolu se zadáním došel i plastový sáček s podezřelým obsahem, je to cukr nebo sladidlo. Pokuste se co nejlépe experimentálně srovnat „sladkost“ (sladivost) dodaného vzorku a několika dalších různých cukrů a sladidel. Pro odměření množství použijte přiloženou lžičku. „Sladkost“ testovaného vzorku určujte pro koncentraci jedné zarovnané lžičky cukru/sladidla v $1\;\mathrm{dl}$ vody. Jako jednotkovou „sladkost“ můžete brát např. rafinovaný řepný cukr (o koncentraci jedné zarovnané lžičky na $1\;\mathrm{dl}$ vody). Porovnávat pak můžete tak, že si připravíte roztoky o různé koncentraci známého cukru/sladidla a budete srovnávat chuť těchto roztoků s připraveným roztokem testovaného vzorku. Pro zpřesnění určení „sladkosti“ se domluvte s nějakými dalšími lidmi, kteří se do srovnávání sladkosti zapojí (ale ne s ostatními řešiteli, ať má každý svoje vlastní řešení). U každého cukru zjistěte co nejpřesněji složení a výsledky vhodně zpracujte.

Nápověda: Cukr se dá sehnat řepný rafinovaný (normální bílý cukr, co se obvykle u nás používá), ale je také k sehnání např. třtinový cukr (chemicky téměř jako řepný), hroznový cukr (dextróza; v Glukopuru) a ovocný cukr (fruktóza). Ze sladidel můžeme jmenovat sorbit, huxol, sukralózu (v Cukrenu, Cukravitu), aspartam (v Irbis big sweet). Ke slazení se také používá med. Doporučujeme použít sladidla s řádově podobnou sladivostí (u některých čistých sladidel, co sladí i 600 krát tolik, co obyčejný cukr, narazíte na problémy s odvažováním). Pokud FYKOS řešíte poprvé a měli byste zájem o vzorek, stačí o něj napsat na emailovou adresu podezrelyprasek@fykos.cz.

Varování: Každá látka může být při zvýšené spotřebě nebezpečná. I destilovaná voda je jed. Snažte se tedy dodržovat doporučené denní dávky.

• Aktivní galaxie se na obloze stejně jako hvězdy jeví jako bodové zdroje. Zkuste navrhnout co nejvíce způsobů, jak rozlišit hvězdu a aktivní galaxii.

• Z rádiového pozorování kvasaru 3C 273 se zjistilo, že shluk hmoty v jetu se pohybuje od aktivního jádra s úhlovou rychlostí $\mu$ = $0.0008 \;\mathrm{rok^{ - 1}}$. Předpokládejte, že shluk se pohybuje v rovině oblohy kolmo na linii pozorování, vzdálenost je $d=440\;\mathrm{hMpc}$, $h$ je Hubbleova konstanta. Vyjádřete zdánlivou rychlost $v_{zd}$.

• Odvoďte, pro jakou hodnotu úhlu $φ$ bude $β_{T}$ maximální?

• Předpokládejme, že supermasivní černá díra v centru galaxie má účinnost 30 %. Kolik energie vyzáří, pohltí-li objekt o hmotnosti Země?