5. Série 8. Ročníku
Termín uploadu: -
1. vesmírná katastrofa
Tři planetky o stejné hmotnosti $M=10^{26}\; \textrm{g}$ jsou umístěny ve vrcholech rovnostranného trojúhelníka o straně $l=100\; \textrm{Gm}$ [gigametry]. Nemajíce počáteční rychlosti nezbývá jim než padat vstříc jisté záhubě. Určete, za jak dlouho se srazí (rozměry planetek zanedbejte).
2. obvod bez zdrojů
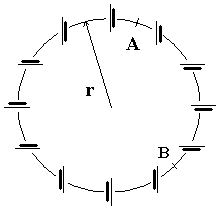
Mějme velmi jednoduchý obvod složený ze $n$ stejných ideálních zdrojů o napětí $U_{e}$ sériově zapojených do kruhu o poloměru $r$. Dráty je spojující mají stejnou délku a měrný odpor $ρ$ na jednotku délky (rozměry zdrojů zanedbejte vůči obvodu kružnice). Jaké bude napětí mezi bodem $A$ uprostřed prvního a $B$ uprostřed $k$-tého drátu?
Na obrázku je nakresleno zapojení konkrétně pro $n=12$ a $k=5$.
3. Ondrova stavebnice
Malý Ondra je na svůj věk velice zvídavý chlapec a místo hraní si s autíčky studuje takřka fyzikálně svět. Ve své stavebnici nalezl dřevěnou kouli a válec o stejném průměru i ze stejného materiálu a jal se dělat pokusy. Vhrnul kouli a válec (bez roztočení, viz obrázek) rychlostí $v_{0}$ po podlaze a sledoval, na jaké rychlosti $v$ se pohyb těles ustálí. Byl velice překvapen, když zjistil, že jedno z těles je rychlejší než druhé. Rozeberte teoreticky jeho „experimentální“ zjištění a určete konečné rychlosti těles. Uvažujte pouze smykové tření s koef. $μ$, valivé tření zanedbejte.
4. kolik máme krve?
Jednou z metod měření objemu kapaliny, jejíž objem se obtížně měří standardními metodami, je následující metoda: Pokusné osobě vpravíme do těla tekutinu o objemu $V_{1}=4\;\mathrm{cm}^{3}$ obsahující radioaktivní atomy $^{24}{\rm Na}$ a o celkové aktivitě $A_{1}=2500\; \textrm{s}^{-1}$. Jelikož poločas rozpadu sodíku 24 je $T=15\; \textrm{hod}$, nemusíme se bát o zdraví měřené osoby. Po čase $t=10\; \textrm{hod}$ odebereme vzorek krve o objemu $V_{2}=10\;\mathrm{cm}^{3}$ a aktivitě $A_{2}=2\; \textrm{s}^{-1}$. Jaké množství krve obsahuje náš pokusný „objekt“?
Poznámka: Pokud neznáte význam veličin psaných kurzívou, zkuste se podívat do nějaké základní učebnice jaderné fyziky.
P. co ten skokan pořád chce
Chceme-li demonstrovat metodu řešení soustavy rovnic na našem skokanovi, budeme muset přidat další podmínku: dejme tomu, že první dopad na prkno se mu zdál příliš tvrdý; rozhodl se tedy rozkývat prkno natolik (změnit amplitudu kmitů), aby druhá srážka s prknem proběhla se zanedbatelnou vzájemnou rychlostí. Tedy jak hodnota Funkce, tak Derivace (uvedená v minulém díle) byla v okamžik srážky rovna nule. Vašim úkolem je najít potřebnou amplitudu $A_{n}$ a dobu druhého skoku $T_{n}$ (odráží se opět dole).
E. chladnutí kapalin
Ve fyzice se často zkoumají tzv. relaxační procesy, tj. postupné ustálení určité fyzikální veličiny na nějaké hodnotě. V termodynamice pod pojmem relaxační doba máme na mysli čas, za který nastane mezi sledovaným systémem a jeho okolím (s nějakou přesností, danou chybou měření nebo fluktuacemi) termodynamická rovnováha. Relaxační doba se samozřejmě mění od procesu, který sledujeme – při vyrovnání tlaků je to asi $10^{-16}\; \textrm{s}$, při různých chemických dějích až měsíce či roky.
Vaším úkolem bude sledovat rychlost chladnutí dvou či více kapalin (např. voda a olej) za stejných okolních podmínek. Aby se vaše práce více podobala skutečnému fyzikálnímu experimentu, proložte naměřenými hodnotami funkci $f(t)=Ae^{-Bt}+T_{0}$ a zkuste interpretovat vypočtené konstanty nebo alespoň odhadněte, na čem by mohly záviset. Pro ty, kdo neví, co je to lineární regrese, je určen krátký odstavec o této metodě.
S. obyčejná
Sestavte program pro iterační metodu a zvolte vhodnou konstantu $k$ pro fci $g$, abyste dostali vhodný interval okolo 1 splňující kontraktivnost. Ověřte lineární konvergenci a zkuste zjistit míru zrychlení při užití Aitkinova procesu.