4. Série 20. Ročníku
Termín uploadu: -
1. nakupujeme minerálky
Určitě jste si v super(hyper)marketu všimli, že plastová láhev oblíbeného nápoje se při rozjetí pohyblivého pásu pokladny začne otáčet a k pokladní ji často musíte postrčit až rukou. Proč to tak je?
Zkuste analyzovat následující modelový případ. Láhev je položena na pás osou kolmo na směr pohybu pásu a láhev i pás jsou v klidu. Náhle se pás rozjede konstantní rychlostí $v=10\, \jd{cm\cdot s^{-1}}$. Jakou výslednou rychlostí se bude pohybovat láhev? Nejdříve analyzujte, jak se budou chovat různé idealizace – jako třeba tuhý válec. Pak si uvědomte, že láhev je plná nápoje, který se nerad otáčí. Pro jednoduchost uvažujte viskozitu nápoje za nulovou, pak se zamyslete nad tím, jak do hry vstoupí viskozita.
Úlohu vymyslel Jano Lalinský na nákupu v TESCU.
2. švestkové víno v číně




V oblíbené čínské restauraci na Vinohradech dávají každému hostu k účtu jako pozornost švestkové víno. Nápoj nalévají do malých keramických mističek s dvojitým dnem (viz obr. 1). Horní dno je skleněné a je pod ním vidět obrázek sedící číňanky (viz obr. 2). Po vypití vína obrázek číňanky zmizí (viz obr. 3). Podrobně vysvětlete, proč se tak stane. Prázdná mistička s vypouklým skleněným dnem je vyfocena na obrázku 4.
Vymyslel Honza po několikáté návštěvě zmíněné restaurace.
3. dostavba Temelína
Odhadněte tloušťku vody potřebnou k odstínění záření z jaderného reaktoru s výkonem $980\, \jd{MW}$ v plánovaném novém bloku JE Temelín. Z celkové energie uvolněné při štěpení jádra uranu připadne zhruba 82 % na kinetickou energii fragmentů, 6 % odnesou neutrina, po 6 % mají neutrony a gama fotony.
Nápověda: Pravděpodobnost, že částice projde materiálem do hloubky $d$, je přibližně rovna $e^{-σnd}$, kde $n=N/V$ je hustota molekul materiálu (v našem případě počet molekul vody v $1\, \jd{m^{-3}}$) a $σ$ je účinný průřez (cross section) pro absorpci částice na molekule. Účinný průřez má rozměr plochy ($\jd{m^2}$, často se užívá jednotka $\jd{barn} = 100\, \jd{fm^2}$) a závisí na energii částic. Hodnoty účinných průřezů se pokuste najít na internetu nebo v příslušných tabulkách.
Úloha řešil Karel Tůma na zkoušce z jaderné fyziky.
4. Kochova vločka
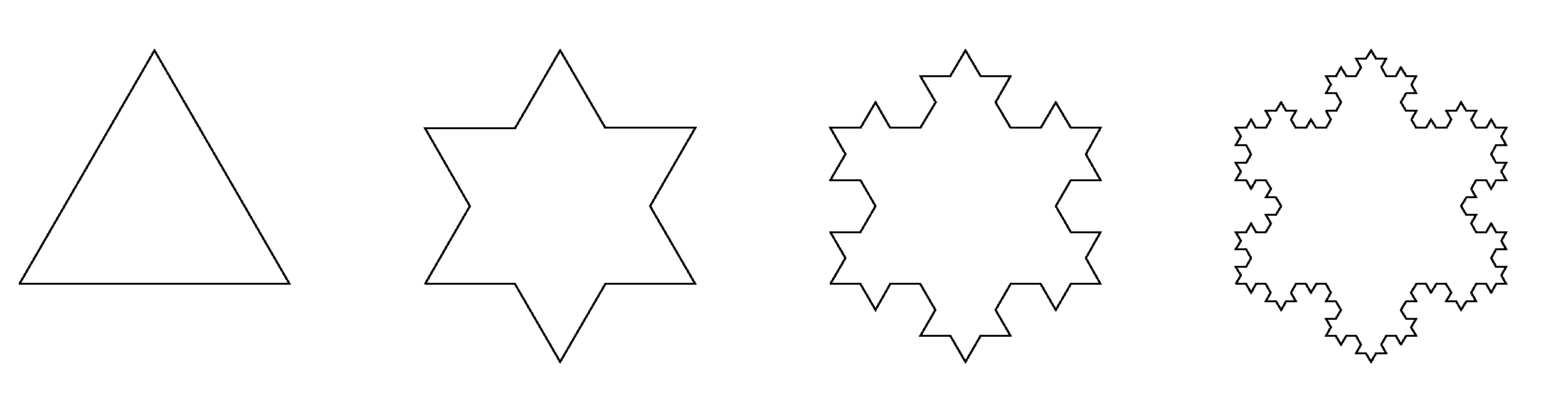
Určete moment setrvačnosti Kochovy vločky zhotovené z homogenního plechu vzhledem k ose kolmé na její rovinu a procházející jejím středem. Uvažujte, že vločka má hmotnost $m$ a průměr $a$.
Poznámka: Kochova vločka je útvar vzniklý iterativním lepením vždy třikrát menších rovnostranných trojúhelníků na strany předchozího útvaru (viz obrázek). Průměrem Kochovy vločky rozumíme vzdálenost vrcholů jejích protějších cípů.
Problém si s chutí vyřešil Marek Pechal.
P. mastný papír
Jistě jste se již setkali s tím, když kapka oleje ukápla na papír. Z bílého papíru se rázem stal papír průsvitný. Vysvětlete, čím to je. Najděte ve svém životě případy, kdy se uplatňuje stejný jev, avšak třeba v úplně jiné situaci.
Na problém narazil Peter Zalom při čtení o sněhových vločkách, když mu kapka oleje dopadla na papír.
E. vytřete nám zrak
Změřte, jak závisí součinitel smykového tření mezi dvěma vámi vybranými materiály na velikosti stykové plochy a na hmotnosti smýkajícího se tělesa. Nezapomeňte nám napsat, s čím a jak jste měřili.
Úloha napadla Honzu Prachaře při čtení Feynmanoých přednášek z fyziky.