3. Série 13. Ročníku

Na pokusné střelnici se nachází vrhač asfaltových holubů. Ve vzdálenosti $d$ od něj stojí myslivec, snažící se zasáhnout letící cíl. Pod jakým úhlem $α$ musí namířit, aby se trefil, víme-li, že na zamíření potřebuje čas $τ$ (tj. čas od vrhu holuba do výstřelu)? Asfaltoví holubi jsou vrháni kolmo vzhůru rychlostí $v_{h}=25\;\mathrm{m}\cdot \mathrm{s}^{-1}$, náboj opouští hlaveň rychlostí $v_{0}=400\;\mathrm{m}\cdot \mathrm{s}^{-1}$, vzdálenost $d=50\;\mathrm{m}$ a čas $τ=2\;\mathrm{s}$. Odpor prostředí zanedbejte.

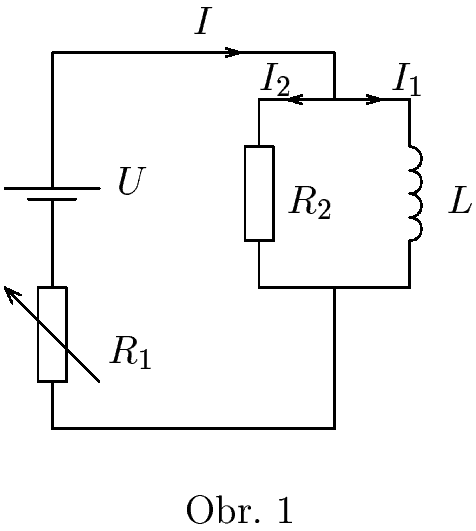
Mějme následující obvod (viz. obrázek). Část obvodu obsahující $R_{2}$ a $L$ $(10\,\jd{H})$je ponořena do kapalného hélia. Vodiče v této části jsou supravodivé (mají nulový odpor). Vyndáme-li $R_{2}$ z hélia, má odpor $5 \,\jd{Ω}$.

První experiment probíhá následovně: Proud $I$ měníme pomocí $R_{1}$ tak, aby v časovém intervalu $(t_{0},t_{1})$ byl konstantní $1 \,\jd{A}$, v $(t_{1},t_{2})$ rovnoměrně klesal na nulu, v $(t_{2},t_{3})$ rovnoměrně stoupal na $0,5 \,\jd{A}$ a dále byl konstantní. V čase $t_{3}$ rezistor $R_{2}$ vyndáme z hélia a v čase $t_{4}$ jej tam opět spustíme. V $t_{0}$ je $I_{1}=I_{2}=0,5 \,\jd{A}$. Určete časový průběh $I_{1}$ a $I_{2}$ v časovém intervalu ($t_{0},t_{4})$.

Druhý experiment probíhá následovně: Na počátku je $R_{2}=0 \,\jd{Ω}$, $I_{1}=0 \,\jd{A}$, $R_{1}=7,5 \,\jd{Ω}$, $I=0,5 \,\jd{A}$. $R_{1}$ se dále nemění. V čase $t_{1}$ vyndáme $R_{2}$ z hélia a v čase $t_{2}$ jej tam opět spustíme. Načrtněte do grafu průběh časové závislosti $I$, $I_{1}$, $I_{2}$.

Uvažte měděný kruhový závit o poloměru $R=10\;\mathrm{cm}$, který leží na stole v magnetickém poli Země (vektor magnetické indukce je rovnoběžný se stolem, který se nachází na rovníku). Poloměr drátu je $r=0,3\;\mathrm{mm}$. Závitem prochází proud $I$. Určete $I$ tak, aby se závit překlopil (předpokládejte, že tření je dostatečně velké, takže závit neproklouzne).

Představme si autíčko, které jede po letišti rovnoměrně přímočaře (vzhledem k letištní hale) rychlostí $v$. Kromě autíčka stojí na letišti sličná letuška (nestojí na přímce, po které se pohybuje autíčko). V okamžiku, kdy je autíčko letušce nejblíže (t.j. spojnice autíčko - letuška je kolmá na$v$), se řidič rozhodne, že dojede letušku navštívit. Autíčko dokáže v libovolném směru vyvinout zrychlení o maximální velikosti $a$. Za jaký nejkratší čas se autíčko dostane k letušce? Čas se počítá od okamžiku fatálního rozhodnutí. Předpokládejte, že auto u letušky nebude zastavovat ani přibržďovat.

(Nápověda: Uvažujte různé vztažné soustavy.)

Spočtěte frekvenci kmitů atomů v krystalu $\,\jd{NaCl}$. Můžete si úlohu zjednodušit tak, že budete uvažovat pouze coulombovské působení sousedních atomů. Jako bonus můžete spočítat i amplitudu výchylky.

Sežeňte si stopky, dostatečné množství lihu (denaturovaného) a neokalibrovaný hustoměr (či dřevěnou tyčku zatíženou závažíčkem), u kterého si můžete zjistit rozměry a hmotnost. Navrhněte vhodnou metodu, ve které použijete zmíněné pomůcky, a změřte hustotu lihu.

Uvažujme reálnou křemíkovou diodu s přechodovým napětím $0,6 \,\jd{V}$ při pokojové teplotě (fyzici pro jednoduchost považují za pokojovou teplotu $300 \,\jd{K}$, oproti normální $20{^\circ} \,\jd{C} = 293 \,\jd{K}$, protože se s tím lépe počítá a lépe se to pamatuje). Pokuste se z uvedených rovnic (i v minulých dílech seriálu) odhadnout, jak se bude dioda chovat při zvýšení teploty o $10 \,\jd{K}$, $20 \,\jd{K}$ a $40 \,\jd{K}$. Není třeba do puntíku počítat, co se přesně stane, jde pouze o kvalitativní odhady. Ti, kdo mají možnost, mohou odhady ověřit měřením – k měření voltampérové charakteristiky je třeba pouze dioda, ochranný odpor (nikdy nezapojujte diodu v propustném směru přímo na napětí!), zdroj napětí, voltmetr a ampérmetr. Odhady by měly být pro přehlednost aspoň schematicky nakreslené v nějakém grafu. Zaměřte se zejména na velikost závěrného proudu a polohu kolena v propustném směru.