5. Série 18. Ročníku
Termín uploadu: -
1. dáreček od Buffala
Buffalo Bill se už roky snaží polapit Jessieho Jamese, známého banditu. V městečku Clay County mu konečně přišel na stopu. Strhla se přestřelka. Buffalo si všiml sudu plného petroleje na vozíku mezi sebou a Jessiem. „Jak dostat sud k Jessiemu, abych ho mohl zapálit,“ rozmýšlí Bill.
Jessie prostřelil sud v 9/10 výšky a ze sudu začal stříkat petrolej. Buffalo se trefil přesně do poloviny sudu a střílí znovu. Vyřešte, s jakým počátečním zrychlením se bude pohybovat vozíček v závislosti na tom, kam se Bill trefí podruhé. Předpokládejte, že hybnost kulky je nulová, a tření zanedbejte. Zamyslete se nad dalšími zajímavými okolnostmi tohoto souboje.
SK olympiáda.
2. pád ze schodů
Malý Karlík si hraje s kuličkou. Při cvrnkání je však neopatrný, kulička se mu odkutálí k nakloněné rovině, kterou doma mají místo schodiště, a začne po ní klouzat dolů. Kulička se pohybuje tak, že vektor její rychlosti $v$ svírá s horní hranou nakloněné roviny úhel $φ$. Vypočítejte vektor rychlosti $v′$ kuličky (tj. jeho velikost a také směr) pod nakloněnou rovinou, jejíž výška je $h$. Tření mezi kuličkou a zemí je malé, proto ho zanedbejte. Předpokládejte, že horní a dolní hrana nakloněné roviny je zaoblená, takže se kulička neodlepí od podlahy.
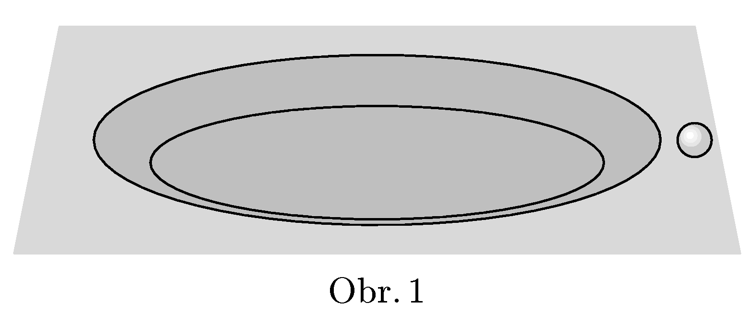
Jako bonus můžete vypočítat, jak se změní směr rychlosti kuličky, která proletí válcovou jamkou o poloměru $R$ a hloubce $h$ se zkosenými hranami (viz obr. 1). Délku zkosení můžete vzhledem k poloměru jamky zanedbat.
Napadlo Matouše.
3. beta rozpad
Při měření rozpadu neutronu na elektron a proton proměřovali čeští vědci energii vylétávajícího elektronu. Jak mohou pouze na základě údajů z tohoto měření poznat, zda nevzniká při tomto rozpadu ještě jiná částice? Uvažujte, že neutron je před rozpadem v klidu.
Pavel Augustinský
4. neposlušná gravitace
Při dlouhodobém pozorování zákrytů Jupiterova měsíce Io bylo zjištěno, že naměřená doba oběhů měsíčku kolem planety (např. od předchozího do následného začátku zákrytu) pravidelně kolísá mezi hodnotami $42\, \jd{h}\, 28\, \jd{min}\, 21\, \jd{s}$ a $42\, \jd{h}\, 28\, \jd{min}\, 51\, \jd{s}$ (s chybou měření $2\, \jd{s}$).
Pokuste se jak kvalitativně, tak kvantitativně vysvětlit pozorované změny. Kvantitou rozumíme určení „velikosti této příčiny“ na základě měření samozřejmě s odhadem chyby!
Pavel Brom
P. rychlejší než voda
Zamyslete se nad tím, zda se může lodička bez motoru na řece pohybovat rychleji než samotná voda. Svou odpověď zdůvodněte a předpokládejte, že proudění vody je laminární.
Kapicova úloha
E. paličův seník
Určete teplotu vznícení náplně plynového zapalovače, tj. nejnižší teplotu, na kterou ji musíme zahřát, aby se na vzduchu vznítila. Jako bonus můžete též zjistit zápalnou teplotu technického lihu nebo jiné organické látky.
Postupujte například tak, že na odporový drát rozžhavený průchodem elektrického proudu pustíte plyn ze zapalovače. K určení zápalné teploty využijete změřené hodnoty napětí a proudu a známou závislost odporu na teplotě. Vaší vynalézavosti se však meze nekladou.
Varujeme: Oheň způsobuje těžké popáleniny, postupujte proto obezřetně!
Pavel Augustinský
S. Merkur, jáma a kyvadlo
V následujících úlohách ověříme vaši znalost všech dosud probraných kapitol mechaniky, tj. Newtonova formalismu, D'Alembertova principu a Lagrangeova formalismu.
- Představte si planetu Merkur obíhající kolem Slunce. Jak známo, jeho eliptická trajektorie se stáčí (posouvá se poloha perihélia), což nemůže být způsobeno gravitační silou $F=κ(mMr)⁄r^{3}$. Dokažte, že když k této síle přidáme dodatečnou centrální sílu $F=C(r)⁄r^{4}$, kde $C$ je vhodná konstanta, celá trajektorie (elipsa) se bude otáčet konstantní úhlovou rychlostí (čili existuje vztažná soustava otáčející se konstantní úhlovou rychlostí taková, že trajektorie v ní bude elipsa). Znáte-li tuto úhlovou rychlost $Ω$, určete konstantu $C$. Stačí takováto oprava k záchraně Newtonovy teorie gravitace?
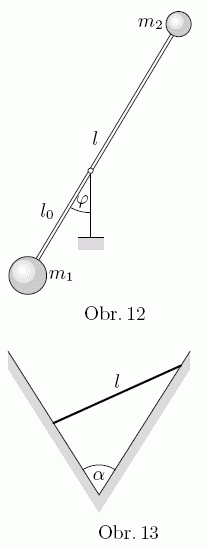
- Určete rovnovážné polohy homogenní tyčky délky $l$ opřené o vnitřní stěny jamky ve tvaru písmene „V“ (viz obr. 12) v závislosti na vrcholovém úhlu jamky $α$.
- Pomocí Lagrangeových rovnic vypočítejte periodu malých kmitů dvojzvratného kyvadla na obrázku 13. Závaží na koncích nehmotné tyčky délky $l$ mají hmotnosti $m_{1}$ a $m_{2}$, vzdálenost bodu závěsu od závaží o hmotnosti $m_{1}$ je $l_{0}$.
Na úlohu (1) narazil Matouš v jedné pěkné ruské knize; (2) a (3) zadal Honza Prachař a Jarda Trnka.