1. Série 19. Ročníku
Termín uploadu: -
1. opravdu Saturn plave?
Věříte, že průměrná hustota Saturnu je menší než hustota vody?
Sami se můžete na Saturn podívat v dalekohledu. Kromě prstence uvidíte kolem planety několik měsíců, pokud nebudou zrovna v zákrytu. (V takovém případě byste si např. na měsíc Titan museli počkat nejdéle 6 hodin, kolik trvá jeho přechod přes kotouč planety.) Můžete zjistit, že Titan oběhne planetu jednou za 16 dní. Dokážete z pozorování měsíce Titanu určit průměrnou hustotu Saturnu? Pokud ne, zdůvodněte, pokud ano, vypočtěte ji a přesvědčíte se o jedné zajímavosti.
Při pozorování Saturnu vymyslel Pavel Brom.
2. Baník, slečno
Fanoušci Baníku jeli do Prahy na Spartu. Policisté však byli po špatných zkušenostech připraveni a do vagónu nainstalovali vodní dělo.
Na půli cesty, když vlak zrovna stál v České Třebové, baníkovci začali demolovat vybavení vagónu (jenž váží $30\, \jd{t}$). Policisté nechali dotyčný vagón odpojit a briskně využili své zbraně. Za minutu na fanoušky vystříkali tisícilitrovou nádrž. O jakou vzdálenost proto popojel vagón dlouhý $30\, \jd{m}$?
Předpokládejte, že vagón je odbržděný a že voda z vagónu může vytékat pouze ve svislém směru. Změnu hmotnosti vagónu způsobenou odtokem vody můžete zanedbat.
Zážitek Honzy Prachaře, když se vracel vlakem domů.
3. Armagedon
Poplach! Rudá světla indikují smrtelnou hrozbu. Směrem k Zemi se řítí meteoroid o známém průřezu $S$ a tepelné kapacitě $c$. Určete, o kolik se zvýší jeho teplota během průletu atmosférou.
Předpokládejte, že se jeho rychlost stačí před dopadem ustálit a že se zahřívá rovnoměrně. Sami odhadněte, jaká část energie se spotřebuje na ohřátí vzduchu v atmosféře. Zamyslete se, jak je tento model realistický. Nakonec rozhodněte, zda bude mít meteoriod vyšší či nižší teplotu, pokud namísto vzduchem poletí vakuem, jež má nulovou tepelnou kapacitu.
Upravená úloha Kájinkova padajícího kulového kladívka.
4. hoďte si smyčku
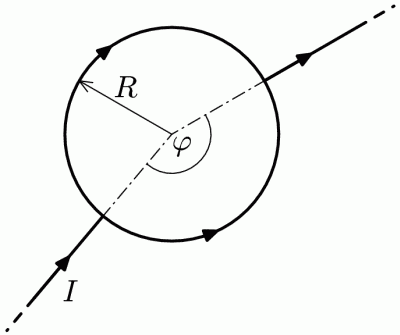
Představte si kruhovou smyčku tvořenou drátem. Radiálními vodiči přivádíme a odvádíme elektrický proud (viz obrázek). Jaké bude magnetické pole uprostřed smyčky? Poloměr smyčky je $R$, úhel mezi radiálními přívodními dráty $φ$ a proud v drátu $I$.
Navrhl Matouš Ringel.
P. příliv na Bali
Když skončila Mezinárodní fyzikální olympiáda na Bali, olympionici odešli na celý den relaxovat k moři na jižní okraj tohoto ostrova v Indonésii. Sledovavše korálový útes, jak mizí v přílivové vlně, uvědomili si po uplynutí úplňkové noci a letního dne, že příliv nastal jen jednou (během 24 h ). Domorodci jim tuto skutečnost potvrdili, ale neuměli ji vysvětlit podobně jako účastníci MFO. Dokážete to vy?
Honza na MFO na Bali.
E. tvrdost kuliček
Až budete jedno podzimní odpoledne hrát s kamarády kuličky, uzměte svým přátelům jednu z nich a mrštěte s ní o tvrdý povrch. Posléze si udělejte značku ve výšce, do které kulička vyskočí, a změřte ji. Z naměřených hodnot určete koeficient odrazivosti kuličky (poměr energie kuličky před odrazem a po něm).
Podobná metoda se používá pro třídění tvrdosti ložiskových kuliček; málo tvrdé kuličky nepřeskočí bariéru a odstraní se.
Lenka
S. pravděpodobnost
- Z balíčku 32 karet se náhodně vyberou tři karty. Zjistěte pravděpodobnosti jevů, že mezi vybranými kartami bude právě jedno eso, alespoň jedno eso, ani jedno eso.
- $N$ stejných částic se nachází v nádobě. Určete pravděpodobnost, že v levé půlce bude o $m$ částic více než v pravé půlce. Nakreslete graf závislosti pro $N=10^{10}$. Rozsah $m$ volte tak, aby pravděpodobnost na krajích intervalu byla desetinová oproti středu intervalu. Jak závisí šířka křivky (tj. rozdíl $m_{2}-m_{1}$, kde $m_{2}>0$ a $m_{1}<0$ jsou hodnoty $m$, pro které je pravděpodobnost poloviční oproti maximu) na $N?$
- Odhadněte velikost ln ($n!)$ (bez použití Stirlingova vzorce).
Autor seriálu Matouš Ringel.