3. Série 22. Ročníku
Termín uploadu: -
1. tlačenice
Organizátoři si z podzimního soustředění odvezli tlakovou nádobu s vodíkem a na vánoční besídce chtějí udělat pokus. Všechen plyn z ní vypustí do lehkého balonu – tj. bude mít atmosférický tlak. Dokáže takovýto balon uzvednout prázdnou tlakovou nádobu, když víte, že teplota zůstává konstantní?
Z maďarské přípravy na FO od Dalimila vybral Aleš.
2. trainstopping
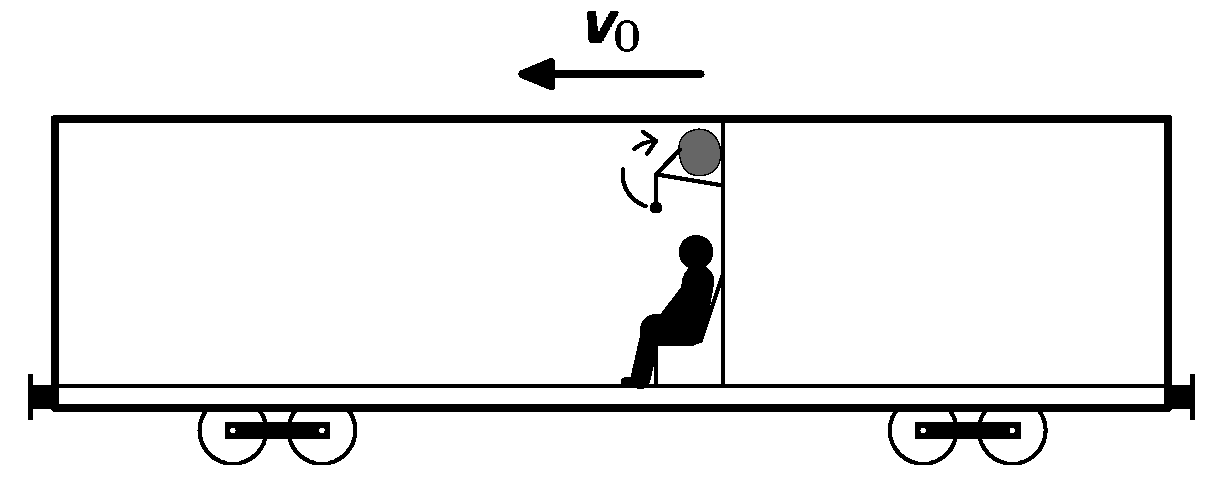
Honza jede domů vlakem rychlostí $v_{0}$. Z poličky na zavazadla mu z batohu visí olovnice. Najednou vlak začne brzdit (zrychlením $a$ po dobu $t)$, protože na železniční přejezd před ním vjel neopatrný řidič. A Honzu napadne – mohla se olovnice s napnutým provázkem otočit o 180 °? Uvažte, že je olovnice pevně zavěšena na poličce.
Z maďarské přípravy na FO od Dalimila vybral Aleš.
3. zachraňte hélium
Na pouti v Dolním Dvoře mají novou atrakci, héliem plněné mýdlové bubliny, které se téměř nehybně vznášejí ve vzduchu. Co je těžší? Hélium v bublině, nebo její stěna?
Z maďarské přípravy na FO od Dalimila vybral Aleš.
4. vánoční řetěz
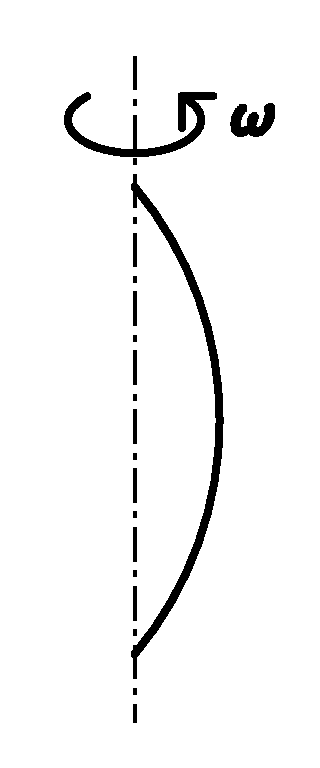
Jakub se o přednášce nudil, z batohu si vytáhl řetízek, chytil jej na dvou místech mezi prsty a začal s ním točit úhlovou rychlostí $ω$ jako na obrázku. Marek to uviděl a zeptal se Jakuba, jaký tvar má rotující řetízek. Co mu Jakub odpověděl, když zanedbal vliv tíhového pole?
Na přednášce vymyslel Jakub Michálek.
P. titanový život
Titan – družice Saturnu – je mrazivý svět (povrchová teplota asi $94\, \jd{K}$) s mohutnou dusíkovou atmosférou, ledovým povrchem a uhlovodíkovými jezery. Radar na sondě Cassini obíhající Titan zjistil, že povrchové útvary rotují rychleji než měsíc sám (asi o $0,36^{\circ} \, \jd{{rok}^{-1}}$). Vědecké zdůvodnění zní, že působením větru se mění rotace ledové vrstvy, která plave na podzemním oceánu. O rotaci měsíce se předpokládá, že je synchronizována s oběhem Titanu kolem Saturnu.
Další indicii podzemního oceánu poslala sonda Huygens, která po oddělení od Cassini přistála na povrchu Titanu. Během klesání atmosférou naměřila relativně silné radiové elektromagnetické vlny o frekvenci asi $36\, \jd{Hz}$. K odrazu a zesílení radiových vln může dojít na vodivém prostředí jako je právě rozhraní vody a ledu pod povrchem.
Poraďte expertům NASA, jakými metodami by mohla současná nebo budoucí sonda k Titanu potvrdit nebo vyvrátit existenci podzemního oceánu.
V aktuálním dění zaujalo Honzu P.
E. ve víně je pravda
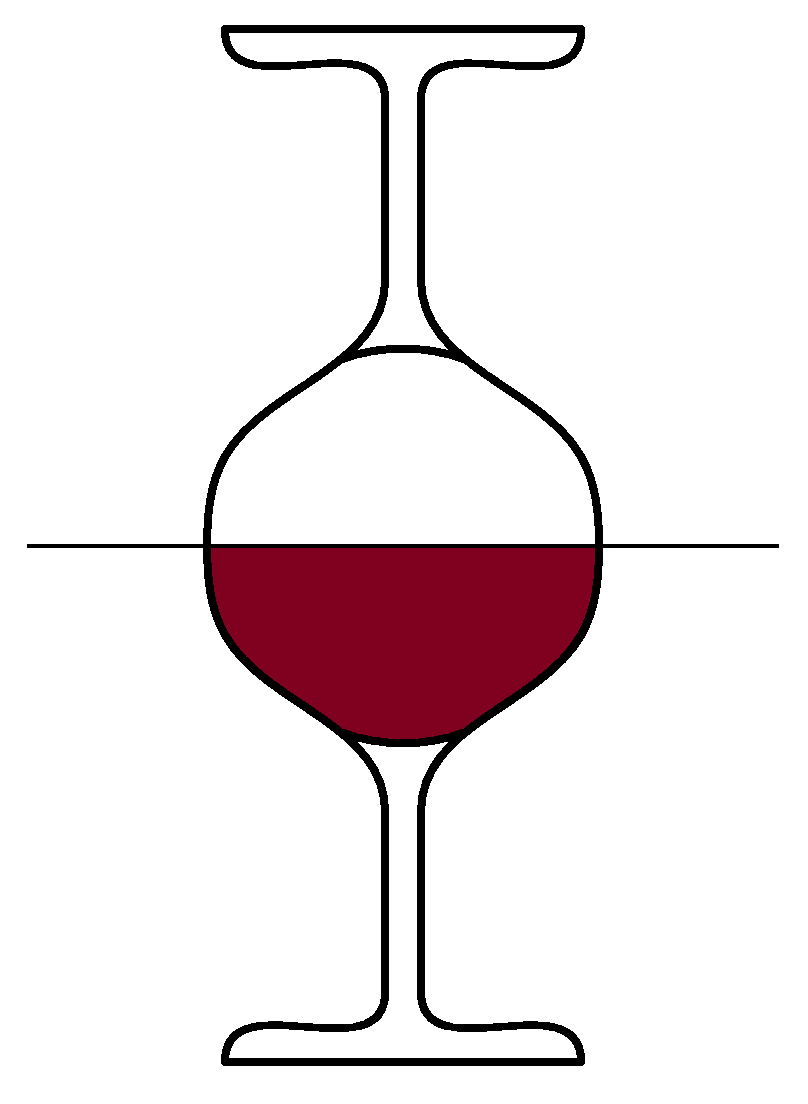
Vyzkoušejte si následující pokus. Naplňte až po okraj stejné sklenice vína a vody. Na tu s vodou položte list papíru, sklenici otočte a položte na sklenici s vínem tak, aby jejich okraje lícovaly (konečný stav vidíte na obrázku). Teď, když opatrně vytáhnete papír tak, aby v kruhu vytyčeném okrajem sklenic vznikla malá mezírka, dojde k zajímavému jevu. Obsahy sklenic se vymění, aniž by se smísily (pokus trvá poměrně dlouho, buďte trpěliví). Zkuste se zamyslet proč, ale hlavně úkaz pořádně prozkoumejte. Zjistěte, jak závisí doba výměny na ploše mezírky, koncentraci alkoholu a jiných parametrech podle vašeho uvážení. Proběhne i pro jiné kapaliny? Například pouze obarvenou vodu, mléko, olej …
Na přednášce na vlastní oči viděl Jakub M.
S. céčková
- Představte si, že vezmete dostatečně silný laser, vyzařující světlo vlnové délky $400\, \jd{nm}$, a posvítíte s ním na Měsíc. Od jeho povrchu se vyzářené světlo odrazí a vrátí se zpět. Předpokládáme-li, že laser vyzařuje skrze kruhový otvor průměru $1\, \jd{cm}$, jaký bude na zemském povrchu průměr paprsku navracejícího se po odrazu zpět? Poradíme vám, že to bude o poznání více, než $1\, \jd{cm}$.
- V této úloze předpokládejte, že éter skutečně existuje a předpovězte, jak by to dopadlo, kdyby Michelson prováděl svá měření jiným způsobem: Jedno rameno by nechal dlouhé $5$ metrů, zatímco druhé by bylo dlouhé $10\, \jd{m}$. Takto připravená aparatura by vytvořila nějaký interferenční obrazec. Poté by Michelson celou soustavou otočil o $90^{\circ}$, takže by si obě ramena vyměnila místa. V průběhu tohoto otáčení by docházelo k posunům interferenčních proužků. (Představte si rotující dvojštěrbinu.) Jak by se v uvedené aparatuře posunuly interferenční proužky při naznačené rotaci? Jak dlouhé by muselo být delší rameno, aby se interferenční proužky vyměnily, tedy aby se rotací maxima posunuly na minima?
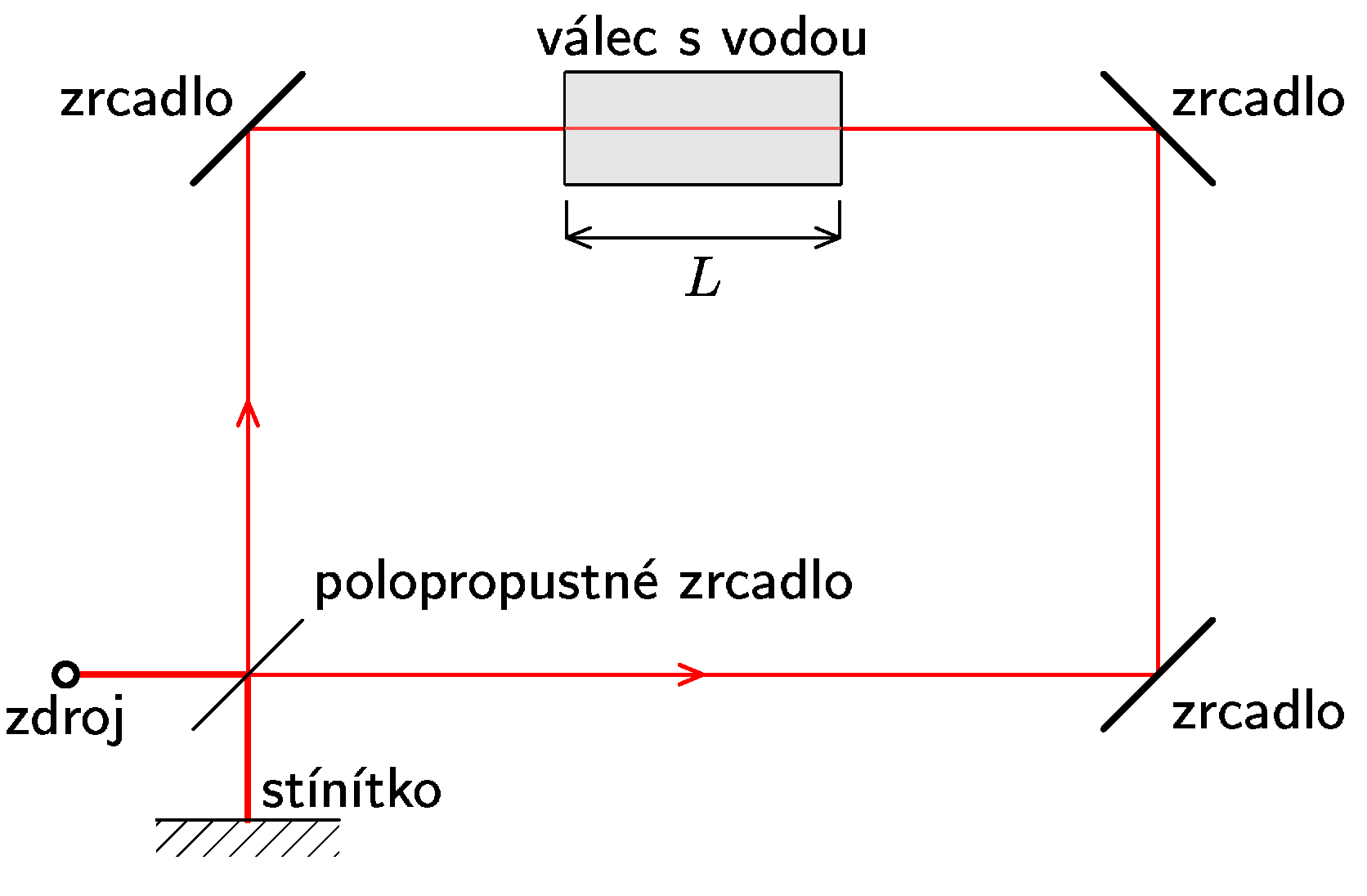
- V následující úloze předpokládejte, že éter existuje a že těleso pohybující se v éteru jej úplně strhuje, takže relativní rychlost tělesa vůči éteru je nulová. Jaký fázový posun by poté vznikl mezi dvěma paprsky v soustavě, naznačené na obrázku? Světlo ze zdroje se na polopropustném zrcadle rozdělí na dva svazky a pokračuje po dokonale obdélníkové dráze zpět na polopropustné zrcadlo, kde vystupuje na stínítko, na kterém sledujeme interferenční proužky. Po cestě jsou oba paprsky třikrát odraženy na zrcadle a procházejí válcem délky $L$, naplněným vodou. Celá soustava kromě válce s vodou (ten je vůči éteru v klidu, nezapomeňte) se vůči éteru pohybuje rychlostí $v$ směrem vpravo.
Zadali autoři seriálu.