3. Série 30. Ročníku
Termín uploadu: -
(3 body)1. dlouhý film
Stahujete si svůj oblíbený film o velikosti $12\; \mathrm{GB}$ rychlostí $10\; \mathrm{MB/s}$. Uvažujte, že signál se po kroucené dvojlince pohybuje rychlostí světla a modulace rozprostírá přenosovou rychlost rovnoměrně, tzn. byla-li by $1\; \mathrm{b/s}$, musíme přijmout signál za celou sekundu k obdržení $1$ bitu informace. Jak dlouhý úsek kabelu dokáže film zaplnit svými daty, pokud se bude šířit dostatečně dlouhým kabelem?
Kolega tvrdil Michalovi, že 100Gb ethernet má rámce menší než čip.
(3 body)2. pekelná
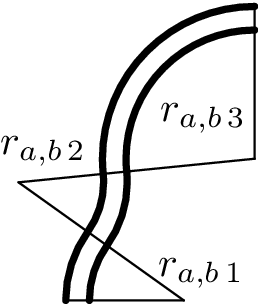
Do pekla vede cesta a silnice po opačných březích řeky. Jdeme po směru řeky, který je vyznačen na obrázku. Břehy řeky jsou tvořeny částmi soustředných kružnic. Pěší cesta kopíruje jeden břeh řeky, silnice druhý břeh, šířka toku je neměnná. Po jaké straně řeky je rychlejší jít? Známe středový úhel každého kružnicového oblouku $φ_{1}$, $φ_{2}$, $…$ a poloměr každé kružnice $r_{a1}$, $r_{b1}$, $r_{a2}$, $r_{b2}$, $…$, kde indexy $a$, $b$ značí levý a pravý břeh.
Napadla Lukáše cestou do Pekla.
(7 bodů)3. kde to píská
Verčiny uši lze aproximovat dvěma bodovými detektory ve vzdálenosti $d$, které detekují zvukové vlny ze všech směrů stejně dobře. Verča umí polohu známého zdroje zvuku poslepu určit velice přesně, proto jednoho dne, když se probudila, vyzvala své přátele k tomu, aby ji vyzkoušeli. Jenže Verča si v jednom uchu zapomněla špunt, který snižuje intenzitu zvuku v jejím levém uchu $k$-krát. Verči byly zavázány oči a zdroj byl umístěn do vzdálenosti $y$ před ni a o $x$ napravo (či $-x$ nalevo). Určete, na které místo $(x',y')$ Verča ukáže, jestliže uši rozeznávají polohu zdroje podle hlasitosti zvuku.
Luboška vyděsil telefon s jedním sluchátkem v uších.
(7 bodů)4. radar zadarmo
Na všechny patníky podél silnice umístěme kontrolní červené tabulky (vlnová délka červené barvy je $λ_\mathrm{č} = 630\; \mathrm{nm}$). Jakmile řidič vidí na patníku před ním tabulku modrou (vlnová délka modré barvy je $λ_\mathrm{m} = 450\; \mathrm{nm}$), ví, že jede příliš rychle. Jaká je tato mezní rychlost? Jakou má běžné osobní auto při této rychlosti hybnost a kinetickou energii?
Kuba našel na internetu futuristickou fotku.
(7 bodů)5. kladkovaná
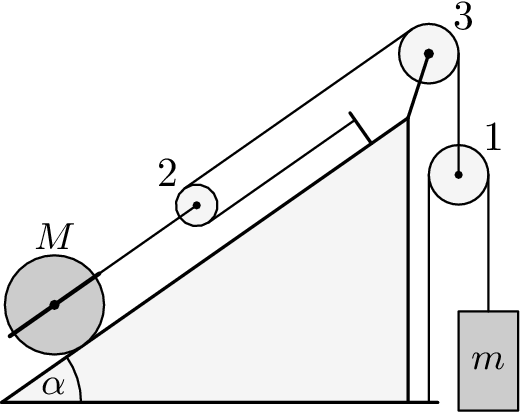
Mějme rozestavení kladek jako na obrázku. Známe hmotnosti $m_{i}$, poloměry $R_{i}$ a momenty setrvačnosti $J_{i}$ všech kladek, hmotnost $m$ závaží a hmotnost $M$, poloměr $R$ i moment setrvačnosti $J$ válce. Zanedbejte tíhu kladky $2$, abyste mohli uvažovat, že lana vedoucí ke kladce $2$ jsou rovnoběžná s nakloněnou rovinou. Součinitel smykového i klidového tření mezi válcem a podložkou je $f$. Lano na kladkách neprokluzuje. Vypočtěte s jakým zrychlením (popř. i úhlovým zrychlením) se bude pohybovat závaží $m$ a válec $M$.
Kubovi přišlo cvičení zbytečně jednoduché.
(8 bodů)P. srdeční
Odhadněte, jakou práci vykoná lidské srdce na pumpování krve za jeden den. S čím se dá tato energie srovnat? Jaké procento z doporučeného denního příjmu energie tvoří váš odhad?
Karlovi se rozbušilo srdce.
(12 bodů)E. reflexní náramek
Změřte co nejvíce charakteristik samonavíjecího reflexního náramku. Zajímá nás především:
- Náramek je vyztužen kusem plechu, který může být ohnut podélně (svinutý náramek) nebo příčně (narovnaný náramek). Jaký poloměr křivosti mají tyto ohyby, pokud na plech nepůsobí vnější síla?
- Pokud náramek narovnáme a budeme ohýbat v jednom místě, při jakém úhlu přejde do ohnutého stavu? Při jakém úhlu se opět narovná? (Pozorujeme hysterezi?)
- Jaký moment síly je potřebný k ohnutí náramku?
- Je některý ze stavů náramku (svinutý nebo narovnaný) energeticky výhodnější? Odhadněte o kolik.
Erikovi se ne a ne ohnout.
(10 bodů)S. limitní
- Zkuste vlastními slovy popsat postup konstrukce intervalových odhadů střední hodnoty v případě obecného rozdělení měřených dat (postačí vlastními slovy popsat následující: centrální limitní věta a předpoklady jejího použití, kovariance a korelace (a jejich odhady), vícerozměrná centrální limitní věta a předpoklady jejího použití, zákon šíření nejistot a kdy ho lze použít). Není potřeba uvádět přesná matematická odvození, stačí požadované pojmy a vlastnosti stručně popsat.
- V přiloženém datovém souboru mereni3-1.csv najdete výsledky měření určité fyzikální veličiny $v$. Předpokládejme, že si nemůžeme být jisti, zda mají měřená data normální rozdělení. Vyjádřete nejistotu měření této fyzikální veličiny (nejistotu typu B neuvažujte), zkonstruujte intervalový odhady na základě CLV a stručně interpretujte jeho význam. Jak by se změnily výsledky a interpretace, pokud bychom měli k dispozici jen čtvrtinu měření (řekněme první čtvrtinu dat z datového souboru)?
- Předpokládejme, že naším cílem je naměřit fyzikální veličiny $x$ a $y$, které budeme chtít využít pro dosazení do vzorce $v = \frac{1}{2} x y^2$. Předpokládejme, že díky znalosti způsobu měření jsme si jisti, že jsou všechna měření na sobě nezávislá a ze zpracování naměřených dat měření máme následující výsledky, které jsou založeny na velkém počtu měření (více než 30 měření každé fyzikální veličiny) $x = (5,\! 2 \pm 0,\! 1)$, $y = (12,\! 84 \pm 0,\! 06)$. Určete odhad fyzikální veličiny $v$ a nejistotu měření fyzikální veličiny $v$.
Nápověda: Mohly by se vám hodit následující vztahy: $$\frac{\partial}{\partial x} \( \frac {1}{2} x y^2 \) = \frac {1}{2} y^2\, ,$$ $$\frac{\partial}{\partial y} \( \frac {1}{2} x y^2 \) = x y \, .$$ * Pomocí simulace ve výpočetním prostředí //R// demonstrujte platnost centrální limitní věty. Tj. generujte $n$-tice nezávislých realizací náhodné veličiny, která nemá normální rozdělení (pro tento případ použijte exponenciální, rovnoměrné a Poissonovo rozdělení s libovolně zvolenými parametry) a na histogramu ukažte, že pokud na data provedeme následující transformaci $\sqrt{n}\frac{\overline{x_n - \mu}}{S_n}\, ,$ takto transformovaná data už budou rozdělena přibližně podle normálního rozdělení $N(0,1)$. (Součástí hodnocení bude i hodnocení vzhledu grafů – zejména vhodně zvolené popisky os a legenda.)
Bonus: Předpokládejme, že naším cílem je naměřit fyzikální veličiny $x$ a $y$, které budeme chtít dosadit do vzorce $$v = x^2 \sin{y}\, .$$ Uvažujme nejobecnější model měření (tj. měřená data nemají normální rozdělení a měření různých fyzikálních veličin na sobě mohou být závislá). V datovém souboru mereni3-2.csv máme výsledky měření fyzikálních veličin $x$ a $y$, určete nejistotu určení veličiny $v$ a zkonstruujte pro ni intervalový odhad.
Michal se pokusil vymyslet limitně těžké zadání seriálové úlohy.