5. Série 2. Ročníku
Termín uploadu: -
1. závažíčko na kouli
Na vrcholu koule poloměru $R$ leží závažíčko, které se v čase nula začne pohybovat. V jaké výšce a kdy se oddělí od povrchu koule?
2. dvě fotografie
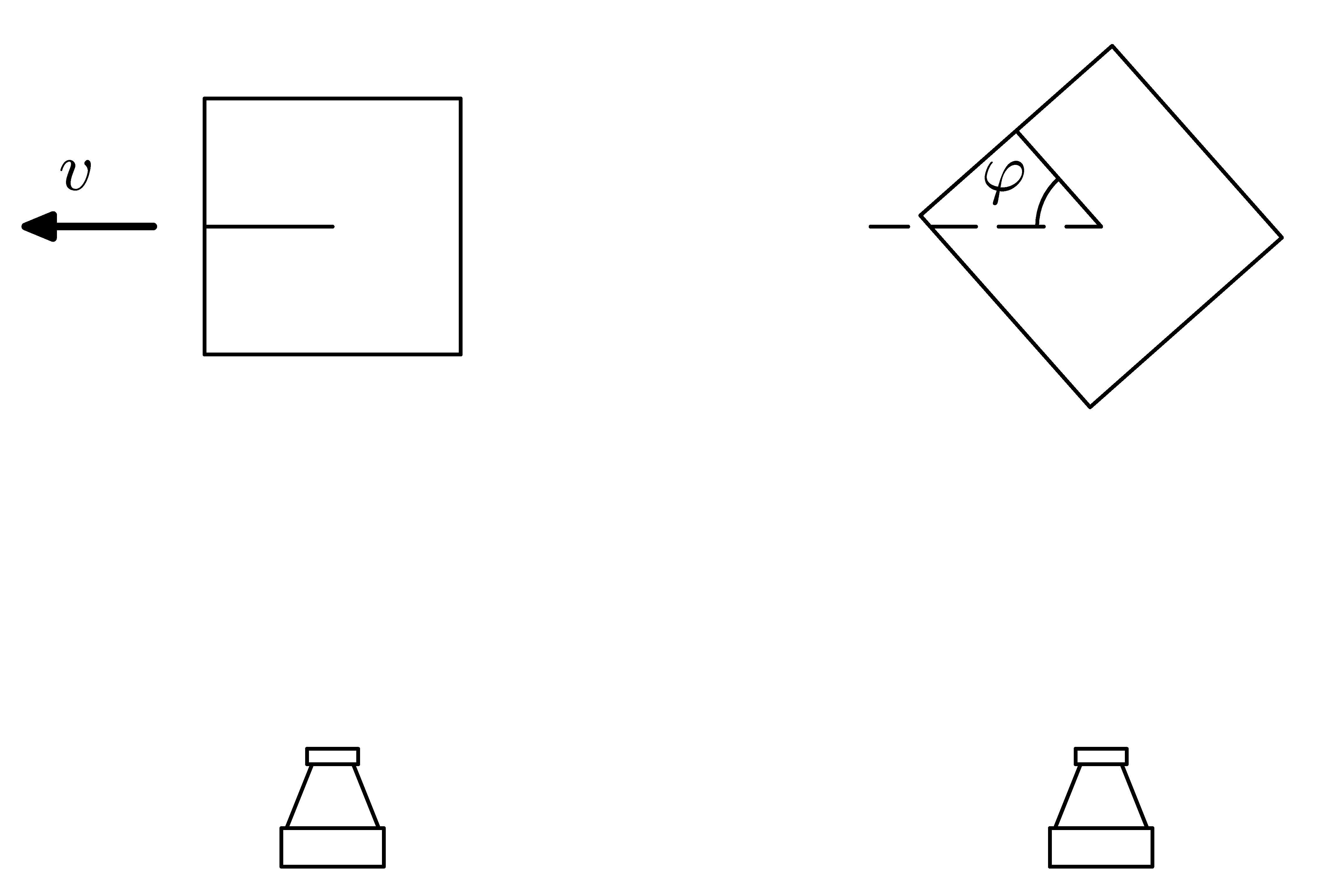
Fotky rakety
Fotograf v některém přístím století vyfotografoval raketu (pro jednoduchost tvaru krychle), a to jednou letící rychlostí blízkou rychlosti světla a jednou stojící, ale natočenou o úhel $φ=48,5°$ (obrázek). S údivem zjistil, že obě černobílé fotografie jsou totožné. Pomozte mu vysvětlit tento jev a spočtěte rychlost letící rakety.
3. nádoby

Nádoby
Ve dvou identických nádobách je na počátku v jedné polovině hélium a v druhé vakuum (obrázek). Obě nádoby jsou rozděleny pístem, v kterém je otevírací kanálek. Nyní provedeme dva pokusy. Kanálek v pístu jedné nádoby otevřeme a plyn přetéká do druhé poloviny nádoby, dokud se nevytvoří rovnováha. Potom píst pomalu přesuneme na kraj nádoby. V druhé nádobě velmi pomalu přesuneme píst ve směru vakua na okraj nádoby.
Srovnejte kvantitativně konečné stavy plynu v obou nádobách. Zanedbejte ztráty tepla přes stěny a tření při pohybu pístu.
4. lokomotivy

Lokomotivy
Lokomotivy určené pro nákladní vlaky jsou jiné než ty, které vozí vlaky s cestujícími. „Nákladní lokomotivy“ jsou přizpůsobeny pro pomalejší jízdu, ale větší nádklady a u „lokomotiv pro cestující“ je tomu naopak. Rozhodněte, která lokomotiva na obrázku je určena pro nákladní vlaky a která pro vlaky s cestujícími.
E. elektrochemický článek
Jedním ze zajímavých elektrochemických jevů je funkce baterie. Nejjednodušeji si elektrochemický článek můžeme představit jako dvě elektrody z různých kovů ponořené do vhodného roztoku či podobného prostředí (elektrolytu). Experimentálně sestavte tabulku napětí mezi elektrodami z různých dostupných kovů ($Fe$, $Cu$, $Zn$, $U$, …). Za elektrolyt zvolte nejoptimálnější běžně dosažitelné prostředí (vybírejte např. z citrónu, jablka, octu, vody, sody, …).
S. Lorentzovy transformace
V posledním seriálovém příkladu se dotkneme transformací snad nejpopulárnějších – Lorentzových transformací. Na přelomu 19. a 20. století bylo přesnými pokusy změřeno, že světlo se pohybuje stejnou rychlostí vůči všem inerciálním soustavám. To zásadně odporuje běžné představě o prostoru a času – odporuje to prosté zkušenosti, že rychlosti se sčítají. Tento problém vyřešil r. 1905 A. Einstein ve svojí speciální teorii relativity. Tato teorie není založena na naší každodenní zkušenosti s malými rychlostmi, a proto se nesmíme zaleknout některých jejích zdánlivě zvláštních důsledků v oblastech, na které nejsme zvyklí. Změna představ na prostor a čas se hlavně odrazila v nahrazení Galileových transformačních vztahů mezi dvěma inerciálními soustavami pohybujícími se vzájemnou rychlostí $v$ ve směru osy $x$, které v čase nula splývají, $x′=x-vt$, $y′=y$, $z′=z$, $t′=t$, se vztahy Lorentzovými. Vaším úkolem bude nyní odvodit je. Využijeme k tomu zkušenosti z pomoci Severním království. Jak bylo v komentáři k seriálovému příkladu 3. série poznamenáno, transformační vztahy mezi $x$, $y$ a $x′$, $y′$ (viz komentář ke zmíněném příkladu) jsou jedinými, které zachovávají vzdálenost, tj. $Δx+(kΔy)=Δx′+(kΔy′)$. Využijeme něčeho podobného. Lze odvodit (provedeme v komentáři), že v našem případě dávají výrazy
$$Δx-(cΔt),Δx′+(cΔt′)\; (1)$$
stejné výsledky. Musíme tedy hledat takové transformace, které převádějí výrazy (1) jeden na druhý. Ve shodě s panem Einsteinem dále předpokládejme, že vztahy mezi souřadnicemi soustav $S$ a $S′$ ($S′$ se pohybuje rychlostí $v$ ve směru $x$ vůči $S$) jsou
$$x′=ax+bt,\; y′=y,\; z′=z,\; t′=cx+dt, \; a,\;b,\;c,\;d∈\textbf{R}\; (2)$$
a pro souřadnice počátku soustavy $S′$ platí $x_{p}/t_{p}=v,\; x_{p}′=0,\; y_{p}′=0,\; z_{p}′=0$. Najděte tedy transformace typu (2), které splňují (1). Uveďte postup!