4. Série 8. Ročníku
Termín uploadu: -
1. částice v magnetickém poli
Nabitá částice vstupuje do prostředí, ve kterém na ni působí odporová síla. Směr této síly je opačný, než směr rychlosti částice, a její velikost je rychlosti přímo úměrná. Než se částice zastaví, urazí v prostředí dráhu $l_{1}=10\;\mathrm{cm}$. Je-li v prostředí navíc homogenní magnetické pole kolmé na směr rychlosti částice, pak se částice zastaví ve vzdálenosti $l_{2}=6\;\mathrm{cm}$ od místa, kde do prostředí vstoupila. V jaké vzdálenosti $l_{3}$ od místa vstupu do prostředí se částice zastaví, když bude magnetické pole dvakrát menší?
2. jak asi táhne komín
Vertikální roura výšky $h=1\;\mathrm{m}$ s plochou podstavy $S=50\;\mathrm{cm}^{2}$ je z obou stran otevřená. V dolní části roury se nachází ohřívač o výkonu $N=100\; \textrm{W}$. Jaká bude rychlost proudění vzduchu v troubě? Lze předpokládat, že veškerý tepelný výkon ohřívače se spotřebuje na ohřátí vzduchu. Atmosférický tlak je $p_{0}=100\; \textrm{kPa}$, teplota okolního vzduchu $t=20\;\mathrm{°C}$. Molární tepelná kapacita vzduchu při konstantním objemu je $C_{V}=2,5\; \textrm{R}$, kde $R$ je plynová konstanta.
3. smyčky a smyčata
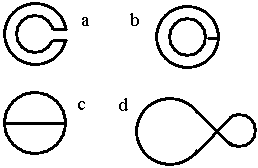
Tvary smyček
V magnetickém poli jsme v rovině kolmé na jeho směr umístili smyčky následujících tvarů (viz obrázek) zhotovené z tenkého odporového drátu. Intenzita pole začne klesat konstantní rychlostí. Jaké proudy potečou v jednotlivých částech smyček?
4. válec kontra zeď

Dřevěný válec o poloměru $R$ a hmotnosti $m$ se valil po podlaze rychlostí $v$ do okamžiku, kdy se zarazil o zeď. O jaký úhel se ještě válec pootočí, než se úplně zastaví? Koeficient tření mezi válcem a stěnou resp. podlahou je $μ$.
P. sférická vada čočky
Spojná čočka má mít tu vlastnost, že svazek paprsků jdoucích z nekonečna rovnoběžně s osou, se zobrazí do jednoho ohniska. Tak je tomu však jen v ideálním případě paprsků jdoucích blízko osy. Uvažujte reálnou čočku s jedním povrchem rovinným a jedním kulovým o poloměru $R$, její průměr jest $D$. V jakém bodě se protnou paprsky dopadající rovnoběžně s osou právě ve vzdálenosti $x$ od osy? Jak velká je oblast těchto bodů na ose? Řešte pro světlo dopadající ze zakulacené strany, případně i pro opačné nasměrování čočky.
S. tečná metoda
Vezměte poslední popisovanou metodu tečen neboli Newtonovu, která určuje následující bod podle vzorce $c=b-\frac{\textrm{funkce}(b)}{\textrm{derivace}(b)}$ – pro ty neznalé derivování uvádíme pro náš případ
$$\textrm{derivace}(t)=-gt+v-\frac{2pA}{T}\sin\left(\frac{2pt}{T}\right)$$
Řešte touto metodou zadanou úlohu a ověřte rychlost konvergence jak pro přesný odhad počátečního intervalu $(0,88;\; 1,02)$, tak pro hrubý odhad $(0;\; 10)$.
Zjistěte, jak závisí přesnost dosaženého výsledku na počtu kroků u všech popsaných metod (bisekce, regula falsi, metoda sečen a tečen), tedy ověřte, zda je zpřesňování lineární, kvadratické, či jiné. Je tato vlastnost ovlivněna volbou počátečního intervalu?