6. Série 8. Ročníku
Termín uploadu: -
1. Jupiter a kometa
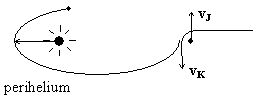
Trajektorie planety
Kometární rodina Jupiteru vzniká následujícím způsobem (viz. obrázek). Kometa přilétá k Jupiteru z velké vzdálenosti s téměř nulovou počáteční rychlostí. Po opuštění Jupiterova gravitačního pole (přesně sféry gravitačního vlivu Jupitera), má její rychlost (vzhledem ke Slunci) přesně opačný směr než rychlost Jupitera. Poté se pohybuje opět v gravitačním poli Slunce. V jaké vzdálenosti od něj se bude nacházet perihelium dráhy komety a jaká je její oběžná doba (jaká je velikost velké poloosy dráhy komety)? Uvažujte, že Jupiter obíhá kolem Slunce po kružnici o poloměru $R=5,2\;\mathrm{AU}$.
2. reálný zdroj
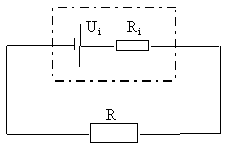
Reálný zdroj elektrického napětí si můžeme namodelovat jako soustavu ideálního zdroje napětí $U_{i}$ se sériově zapojeným odporem $R_{i}$ (viz obrázek). K tomuto zdroji je připojen spotřebič (zátěž) o odporu $R$. Nakreslete graf závislosti celkového výkonu, vnějšího výkonu (spotřebě v zátěži) a účinnosti obvodu (podílu těchto) v závislosti na odporu spotřebiče. Zjistěte, při jakém odporu $R$ jsou uvedené veličiny extremální, a rozhodněte, kdy je vhodné příslušnou hodnotu $R$ použít.
3. před plechem, za plechem
K oblíbeným položkám v matfyzáckém folkloru patří tento zvyk. Zahlédne-li takové indiviuum dlouhou stěnu z vlnitého plechu (nebo jiného podobně tvarovaného materiálu), postaví se cca. $5\; \textrm{m}$ od ní a silně dupne. Ozve se (kromě obvyklého plesknutí) delší drnčivý zvuk, který postupně mění svou výšku.
Vysvětlete, jak tento zvuk vzniká, a spočtěte, jak se mění jeho frekvence s časem. Jaká je doba, po kterou ji slyší? Tvarování plechu je ukázáno na obrázku.
4. expozice
Začínající fotograf, znalec geometrické optiky, fotografoval s určitou expozicí průčelí domu ze vzdálenosti $100\; \textrm{m}$. Potom přešel do vzdálenosti $50\; \textrm{m}$, aby mohl udělat větší snímek. Domníval se (znaje přitom, že plocha domu se zvětší čtyřikrát), že musí expozici zvětšit také čtyřikrát. Doma zjistil, že první snímek se povedl perfektně, ale druhý, na kterém měla být původně i lepá dívka, se nevyvedl. Kromě evidentního důvodu, že to zapříčinila její oslnivá krása, uveďte ten méně podstatný.
E. hustota vzduchu
Pokuste se experimentálně určit hustotu vzduchu, pokud máte k dispozici dva různě velké balónky napuštěné plynem lehčím než vzduch. (Nevíme, jak je to s pouťovým šílením v této době jestliže neseženete vhodný plyn, např. vodík, zkuste použít horký vzduch – chyba měření bude ovšem ďábelská. Případně můžete měřit s plynem těžším vzduchu).
Nápověda: Neznámé hustoty náplně balónku se při výpočtu zbavíte právě tím, že provedete měření pro dva různé balónky, čili ze dvou rovnic tuto neznámou vyloučíte.
S. hledání kořenů polynomu
Napište (a zašlete) program, který určí všechny kořeny polynomu. S jeho pomocí nalezněte čtyři řešení rovnice $x^{4}+2x^{3}+5x^{2}–4x+3=0$.