2. Série 10. Ročníku
Termín uploadu: -
1. rohové zrcadlo
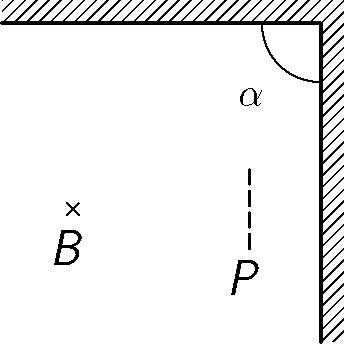
Představte si, že stojíte v bodě $B$ na obr. 1 před dvěma zrcadlovými plochami, které jsou na sebe kolmé ($α = 90°$). Kolikrát uvidíte svůj obraz v zrcadlech? Co se stane, dáme-li před jednu stěnu překážku $P$ (např. skříň)? Jak se situace změní, budou-li zrcadla měnit svůj úhel ($α < 90°$), resp. ($α > 90°$)?
2. magnetické kyvadlo

V homogenním tíhovém poli (tíhové zrychlení $g=9,81\;\mathrm{m}\cdot \mathrm{s}^{-2})$ je na závěsu zanedbatelné hmotnosti délky $l=1,00\;\mathrm{m}$ umístěna malá kovová kulička o hmotnosti $m=10,0\; \textrm{g}$. Na kuličku byl přiveden náboj o velikosti $Q=5,0\; \textrm{μC}$. Celá tato aparatura se nachází ve svislém homogenním magnetickém poli, jehož vektor magnetické indukce $\textbf{B}$ o velikosti $B=0,5\; \textrm{T}$ má stejný směr jako tíhové zrychlení $\textbf{g}$. Vnější magnetická pole jsou vůči tomuto magnetickému poli zanedbatelná. Celá soustava se nachází v klidu. Závěs vychýlíme o úhel $α = 7°$ a uvolníme. Popište pohyb kuličky po uvolnění.
3. jarový tryskáč

Matouš si vystřihl z tvrdého papíru lodičku, která je nakreslena na obr. 3 při pohledu shora. Do místa $A$ pak kápl kapičku jaru a loď spustil na vodní hladinu. Nemálo se podivil, když loď sama od sebe vyrazila prudce vpřed. Umíte pohyb lodi vysvětlit? Platí pro něj zákon zachováni energie?
4. zrcadla, aneb kdo je nejkrásnější
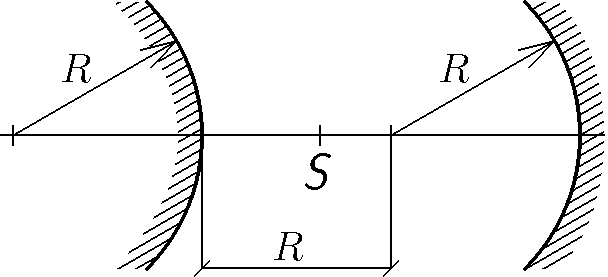
Vypuklé a duté zrcadlo mají stejný poloměr křivosti $R$. Vzdálenost mezi vrcholy zrcadel je $2R$. V jakém bodě na optické ose zrcadel musíme umístit zdroj světla $S$, aby po odraze od vypuklého a dutého zrcadla splýval obraz bodu $S$ se svým vzorem?
P. dvojčata ve vesmíru
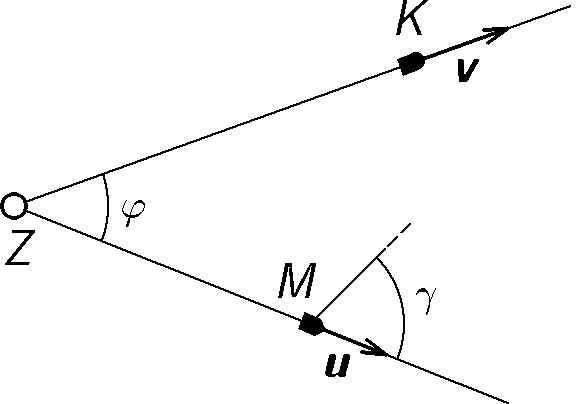
Michal a Karel jsou dvojčata. V zájmu vyššího vědeckého poznání je posadíme každého do jiné kosmické lodi v týž čas $t = 0$ a vystřelíme ze Země $Z$ rychlostmi $\textbf{u}$ a $\textbf{v}$ vstříc hvězdným dálavám. Abychom jim život co nejvíce znepříjemnili, jejich rychlosti svírají úhel $φ$, jak je to vidět na obr. 5. Po čas hvězdného putovaní se jejich rychlosti nemění. V čase $t_{0}$ se Michal, který se zrovna nachází v bodě $M$, rozhodne vyslat zprávu – radiový signál svému sourozenci. Pod jakým úhlem $γ$ vůči svému směru pohybu musí zaměřit signál, aby Karel zprávu obdržel?
Vliv ostatních těles na dráhu lodi a paprsku zanedbejte. Diskutujte též případ, kdy vesmírné lodě nejsou vypuštěny ve stejný čas, ale Michal se vydá do vesmíru o dobu $T$ dříve. Jak se změní výpočet budou-li velikosti rychlosti $\textbf{u}$ a $\textbf{v}$ blízké rychlosti světla $c$?
E. kostka cukru
Zjistěte, jaký tlak vydrží kostka cukru, tj. jaká je její mez pevnosti v tlaku. V řešení nezapomeňte uvést parametry použitých kostek (rozměry kostky, značku cukru apod.). Vhodnou metodou proveďte tolik měření, aby vaše výsledky byly průkazné (nejméně deset měření na jeden druh kostky). Z výsledků zkuste vyvodit nějaké závěry, můžete např. odhadnout práci potřebnou na rozdrcení kostky cukru na cukr krystal.
S. oběžná dráha Země kolem Slunce
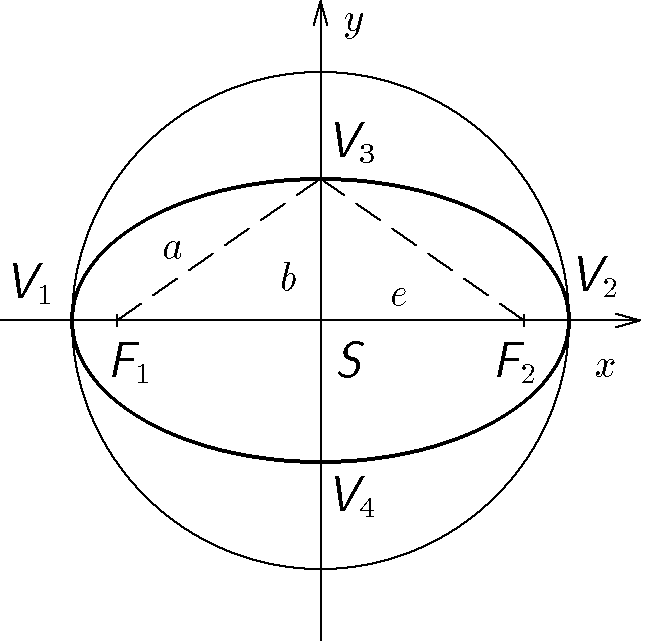
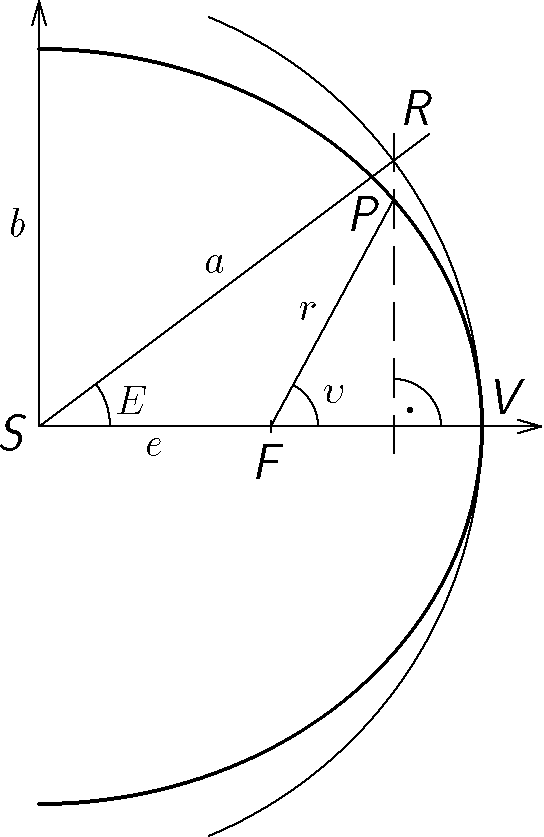
Určete pravou anomálii a vzdálenost Země od Slunce po $1/4$ oběžné doby Země kolem Slunce od průchodu Země periheliem. Velká poloosa je $a=1\;\mathrm{AU}$ a excentricita $e=0,0167$.