5. Série 12. Ročníku
Termín uploadu: -
1. jehla na vodě
Určete maximální průměr ocelové jehly, která se ještě udrží na vodní hladině. Jehla je pokryta tenkým olejovým filmem, aby ji voda nesmáčela. Znáte hustotu oceli, vody a povrchové napětí vody. Pokud řešení problému závisí na délce jehly, pokládejte ji za známou a diskutujte její vliv.
2. dvě láhve
Dvě láhve, jednu plnou vody a jednu prázdnou, necháme kutálet po nakloněné rovině. Která se skutálí rychleji? Pokud ty samé láhve vyšleme se stejnou počáteční rychlostí po nakloněné rovině nahoru, která se dokutálí výše?
3. nákladní auto
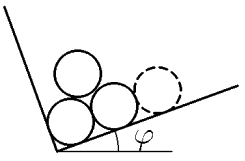
Nákladní auto bylo naloženo stejnými hladkými kládami. Před jejich vykládkou zastavilo tak, že pravými koly stojí o poznání výše než levými (příslušná přední a zadní kola jsou ovšem ve stejné výšce). Řekněme, že rovina nákladního prostoru svírá s horizontální rovinou úhel $φ$, viz obrázek. Po vykládce zbyly na autě tři klády tak, jak je na obrázku nakresleno plnou čarou. Na jakou hodnotu by se musel snížit úhel $φ$, aby se klády přeuspořádaly tak, že by ležely vedle sebe? Jakékoli tření zanedbejte.
4. kulička a nakloněná rovina
Dokonale pružnou ocelovou kuličku spustíme z výšky $h$ (měřeno od místa dopadu) na nakloněnou rovinu, svírající s vodorovnou rovinou úhel $α$. Ve vzdálenosti $d$ od místa dopadu kuličky (ve směru klesání roviny) je svislá stěna. Určete jak vysoko (nad místem dopadu) v ní musíme udělat otvor, aby jím kulička proletěla. Řešte nejprve obecně a pak pro hodnoty $h=50\;\mathrm{cm}$, $d=15\;\mathrm{cm}$, $α=15^{\circ}$. Diskutujte pohyb kuličky v případě, že nakloněná rovina je nekonečná a kuličce nic v cestě nestojí.
P. nabitá koule
Mějme rovnoměrně nabitou kovovou kulovou slupku s poloměrem $R$ a s celkovým nábojem $Q$. Rozřízněme ji na dvě části rovinou, která je od středu koule vzdálena $d<R$. Úkolem je spočíst sílu, jakou se obě části budou odpuzovat, dokud jsou velmi blízko sebe.
E. listopad
Když vezmeme list papíru a pustíme jej ve vodorovné poloze, začne pomalu padat. Pokud jej přehneme na polovinu, bude padat rychleji – toť známý fakt. Vaším úkolem je pomocí tohoto jevu zjistit, podle jakého vztahu se mění odporová síla vzduchu působící na papír (závisí na rychlosti lineárně či kvadraticky?). Pokuste se určit potřebné konstanty.
S. synchronizace módů (mode-locking)
Předpokládejme modově synchronizovaný laser s optickou délkou rezonátoru $l=1,8\;\mathrm{m}$, pracujícího na střední vlnové délce $λ=800\,\jd{nm}$ se středním výkonem $1\,\jd{ W}$.
- S jakou frekvencí laser produkuje jednotlivé pulsy? Jaká je mezi nimi prostorová vzdálenost?
- Jak je prostorově dlouhý puls o délce $70\,\jd {fs}$?
- Kolik fotonů je v jednom pulsu?
- Jaký je špičkový výkon v pulsu?
- Kolik módů potřebujeme k dosažení pulsů o délce $70\,\jd {fs}$? V jaké oblasti vlnových délek musí zesilovat aktivní prostředí? Předpokládejte stejnou amplitudu všech módů, které se účastní tvorby pulsu.
A protože tento díl seriálu byl předposlední soutěžní a vždy jsem se na něco ptal já vás, dám vám tentokrát možnost, abyste se zeptali vy. Napište mi s dalším řešením, co vás z optiky zajímá, co byste si rádi přečetli v posledním dílu seriálu, který vyjde až s řešením 5. a 6. série a už nebude obsahovat žádné úlohy. Pište prosím na zvláštní papír a výrazně jej označte „Co chci vědět z optiky“.