3. Série 18. Ročníku

Průměrná teplota na povrchu Země je $T = 287\, \jd{K}$. Jaká bude nová průměrná teplota $T'$, pokud se střední vzdálenost mezi Zemí a Sluncem zkrátí o 1 %?

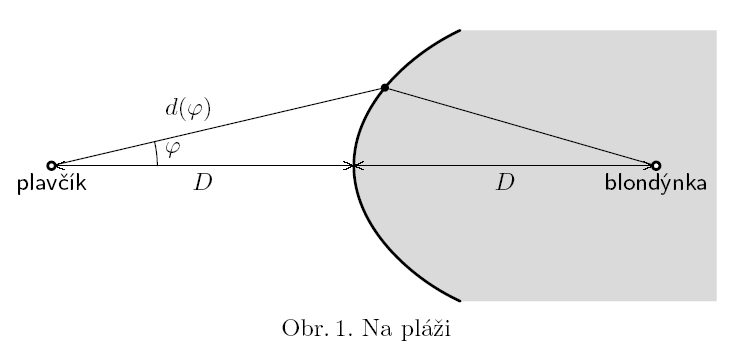
Plavčík stojící ve vzdálenosti $D$ od břehu moře náhle spatří topící se bujnou blondýnku, která doplavala do vzdálenosti $D$ od břehu (viz obr. 1). Poraďte mu, jak se k ní má co nejrychleji dostat, pokud jeho rychlost běhu je $v$ a rychlost plavání $v/2$. Vzdálenost okraje moře od plavčíka závisí na úhlu $\varphi$ se spojnicí plavčíka a blondýnky následujícím předpisem $$d(\phi) = \frac{D}{3}\left( 8\cos{\phi}- {2\sqrt{16\cos^2{\phi}-12\cos{\phi} -3}}-3\right)$$

Jaký je poměr hodnot elektrostatického potenciálu ve vrcholu a ve středu nevodivé rovnoměrně nabité krychle? Celkový náboj na krychli je $Q$ a délka strany krychle je $a$. Předpokládejte, že elektrický potenciál v nekonečnu je nulový.

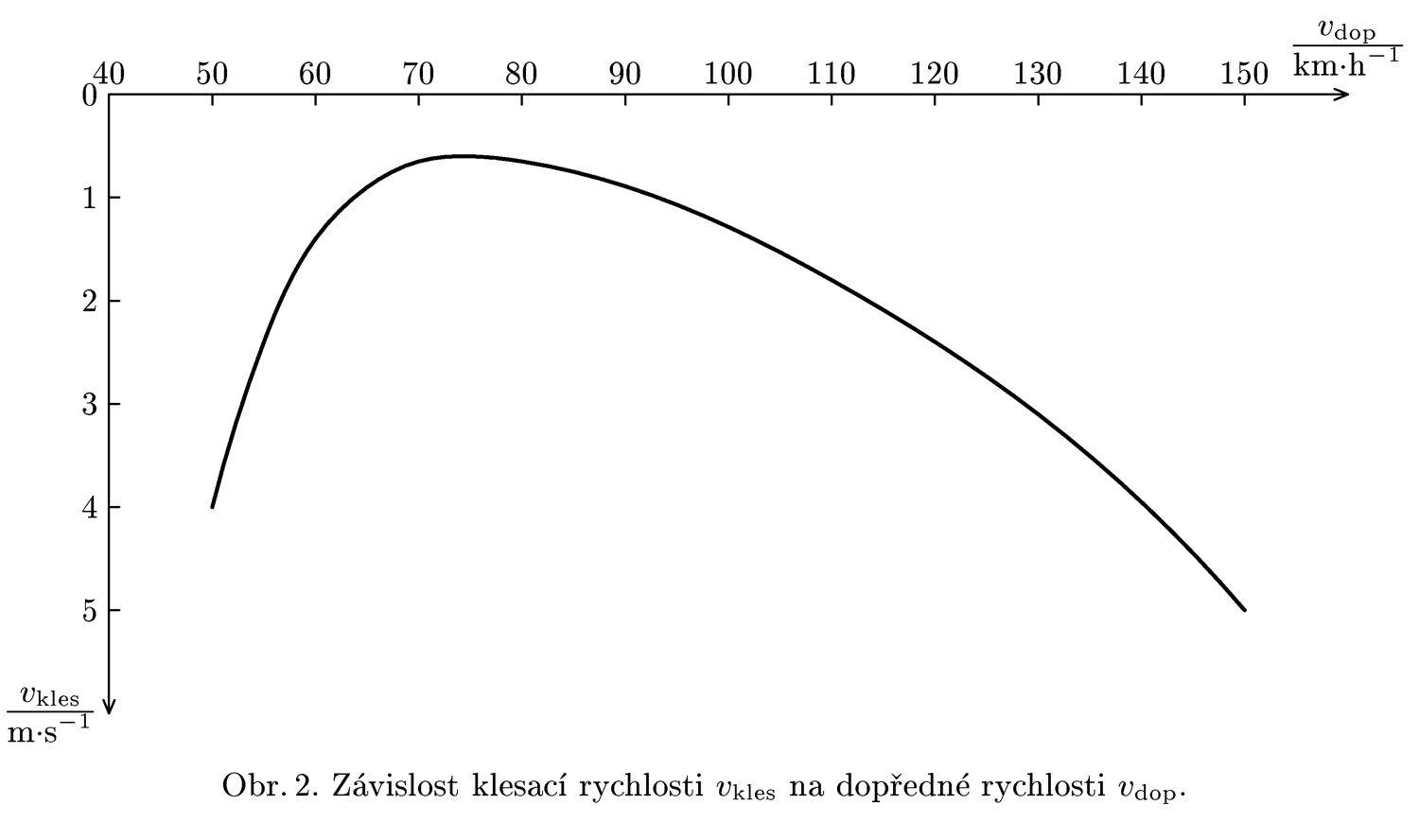
Jeden známý letec se rozhodl ve větroni přeletět kanál La Manche. V Calais se nechal vyvléci do výšky $h = 3\, \jd{km}$ a z této výšky se přímým klouzavým letem vypravil do Anglie. Jako dobrý pilot ví, kterak při ustáleném letu vypadá závislost klesací rychlosti $v_{kles}$ na dopředné rychlosti $v_{dop}$ (viz graf na obr. 2). Poraďte mu, jak rychle má letět, aby doletěl co nejdál.

Když je ve třech čtvrtinách cesty do Anglie, začne od ostrovů fučet silný vítr o rychlosti $10\, \jd{m \cdot s^{-1}}$. Rozhodněte, jak rychle má letět nyní, aby se dostal co nejdál. Jaká by musela být rychlost větru, aby mu znemožnila přistát na pevnině, případně aby mu umožnila návrat do Francie?

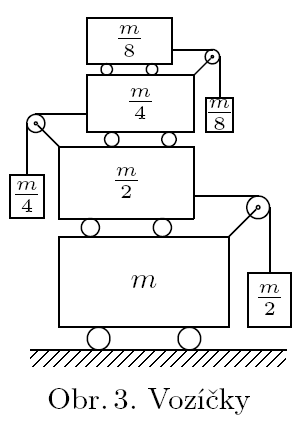
Určete zrychlení prvního a stého vozíčku odspodu na obrázku 3. Vozíčků je nekonečně mnoho, na obrázku jsou zakresleny jen první čtyři. Spodní vozíček má hmotnost $m$, další vozíček, který po něm jezdí, a závaží, se kterým je spojen, má hmotnost $m/2$. Podobně další vozíček a závaží má hmotnost $m/4$, atd. Předpokládejte, že jsou závaží připevněná k vozíčkům, tj. že se ve svislém směru neodchylují. Tření mezi jednotlivými vozíčky zanedbejte.

Změřte hustotu vzduchu. Provést to můžete libovolnou metodou, nezapomeňte k vaší metodě uvést potřebnou teorii. Správný experimentální výsledek nesmí také postrádat určení chyby změřené hodnoty.

Mějme hmotný bod zavěšený na nehmotném a nepružném vlákně.

1. Zaveďte kartézskou souřadnicovou soustavu a v ní napište vazebnou podmínku pro hmotný bod.
2. Napište Lagrangeovy rovnice 1. druhu pro hmotný bod z předchozí části. Ukažte, že jsou ekvivalentní s rovnicí matematického kyvadla $\frac{\rm{d}^{2} \varphi}{\rm{d}t^{2}} + \frac{g}{l} \sin \varphi = 0$, kde $\varphi$ je úhlová výchylka z rovnovážné polohy.
3. Malé těleso je v klidu na vrcholu polokoule a začne klouzat dolů. Pomocí Lagrangeových rovnic 1. druhu určete, v jaké výšce se těleso odlepí od polokoule. ( Nápověda: Těleso se odlepí v okamžiku, kdy $\lambda = 0$.)