1. Série 22. Ročníku
Termín uploadu: -
1. klouzání a kmitání
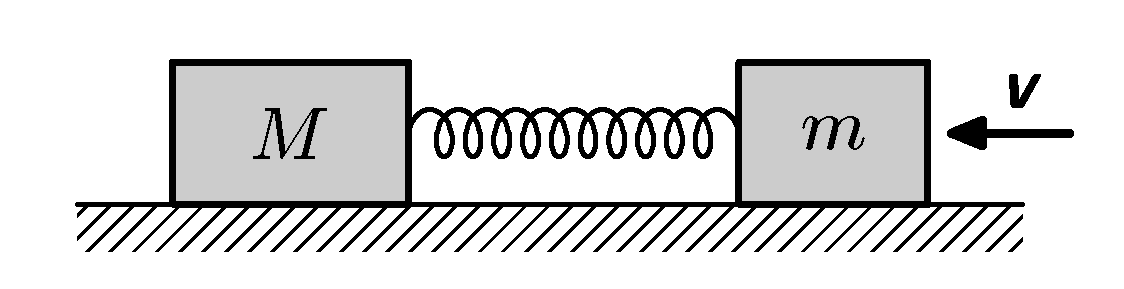
Dvě závaží o hmotnostech $m$ a $M$ jsou spojena pružinou o tuhosti $k$ a leží na hladké podložce (tření můžeme zanedbat). Tělesu $m$ udělíme rychlost $v$ (viz obrázek). Jaká bude nejkratší vzdálenost mezi tělesy a kdy jí dosáhnou?
V ročenkách kanadské FO našel Honza Prachař.
2. pirát a zlatá odměna
Jeden pirát má za odměnu dostat pytel zlaťáků. Ale kapitán lodi je lakomý a chce mu to zkomplikovat. Přetavili zlato do válce. A k tomu ještě odlili druhý, velikostně stejný válec z mosazi. Protože uprostřed zlatého je vzduch, váží oba stejně a jsou stejně velké. Jak si má dotyčný pirát vybrat, aby pak nelitoval?
Úlohu vymyslel kolega Mirka Beláňe.
3. už mě nehoupej
Kačenka se rozhoupává na houpačce následujícím způsobem. Při největší výchylce houpačky se přikrčí, a když je houpačka v nejnižším bodě, opět se postaví. Tyto pohyby neustále opakuje. Poměr vzdálenosti těžiště Kačenky od osy otáčení při pokrčení a při stání je $2^{1⁄12} ≈ 1,06$. Kolikrát se Kačenka zhoupne, než se amplituda houpání zdvojnásobí?
Z asijské olympiády přinesl Honza Prachař
4. praktická motoristická
Na nepřehledných křižovatkách či v ostrých zatáčkách někdy bývá vypuklé zrcadlo. Snadno si všimneme, že zrcadlo zkresluje jak vzdálenost, tak i rychlost přijíždějících aut. Naši vzdálenost od zrcadla označíme $d$, vzdálenost přijíždějícího auta od zrcadla $L$, jeho skutečnou rychlost $v$ a poloměr křivosti zrcadla $R$.
Na základě toho, co vidíme v zrcadle, určete, jak daleko se nám přijíždějící auto jeví? Jakou zdánlivou rychlostí se přibližuje? A jak se liší skutečná doba, za kterou přijíždějící auto vjede do křižovatky, od doby, kterou odhadneme z jeho zdánlivé vzdálenosti a zdánlivé rychlosti? Zvolte si rozumné hodnoty parametrů a rozhodněte, zda může být tento rozdíl dob nebezpečný.
Při cestě na soustředění zažil Marek Scholz.
P. Mikuláš vs. Klaudios
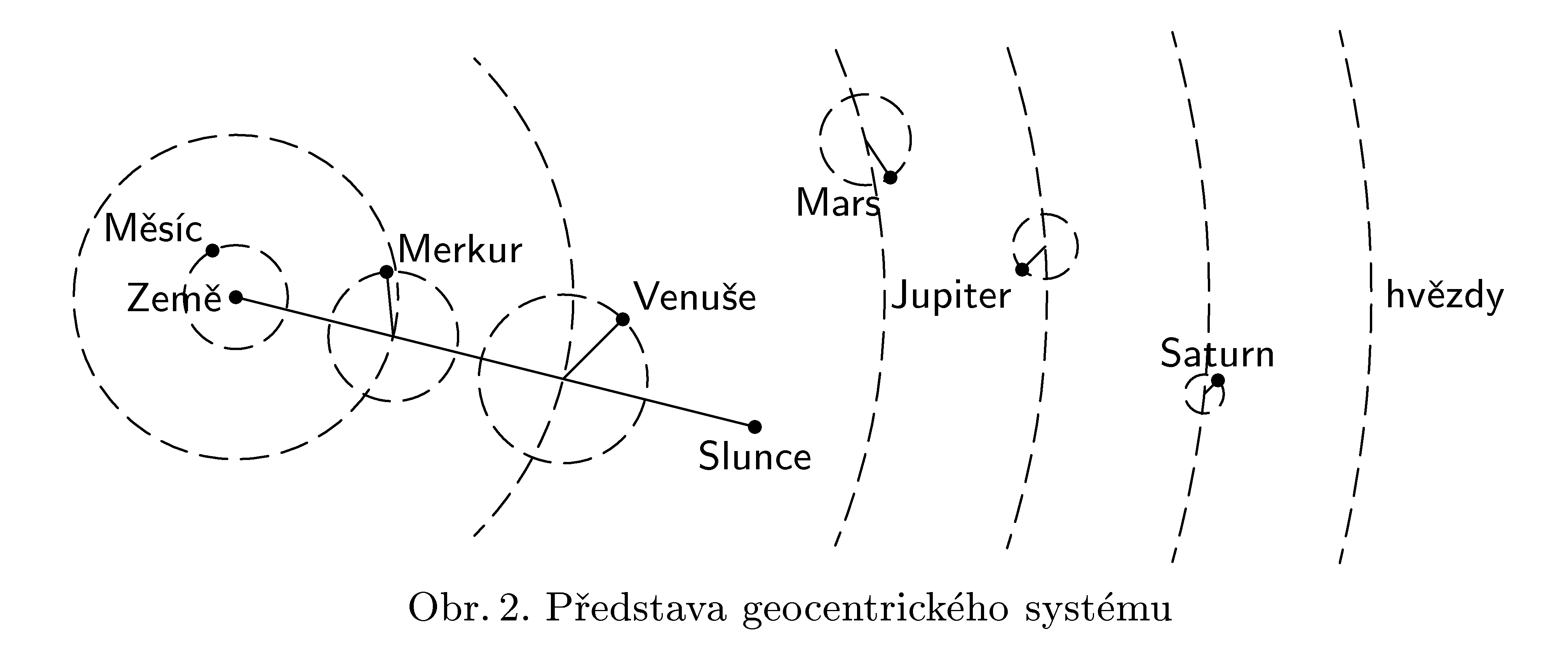
Představa geocentrického systému
Rok 2009 je vyhlášen jako Mezinárodní rok astronomie a připomíná 400 let používání dalekohledů lidstvem. Vraťme se o čtyři staletí zpět, kdy byl dalekohled již k dispozici, ale klasická fyzika ještě v plenkách. V otázce uspořádání světa spolu soupeřily Koperníkův heliocentrický názor a Ptolemaiův geocentrický systém. Navrhněte experiment, resp. pozorování, které mezi oběma představami dokáže rozhodnout. Dostatečně okomentujte, jaký výsledek lze očekávat a co z něj plyne v prospěch či neprospěch uvažovaných uspořádání. Vlastní pozorování není nutné, i když vhodné. Navíc vysvětlete, proč jsou v geocentrickém modelu Slunce a Země spojeny úsečkou?
Významný důkaz chtěl připomenout Pavel Brom.
E. copak nám to tady smrdí?
Změřte rozdíl hustot čerstvého a zkaženého vejce a zjistěte i její časovou závislost! Pokuste se také vysvětlit své výsledky a zvažte užití statistického zpracování.
Tip. Vejce se rychle zkazí například na sluníčku.
S. princip ekvivalence
- Jaké by musely nastat podmínky, aby Galileův pokus nevyšel? Šikmá věž v Pise je vysoká $h =55\, \jd{m}$, předpokládejte, že obě koule mají poloměr $R = 8\, \jd{cm}$ a že jedna koule je vyrobena z olova o hustotě $ρ = 11300\, \jd{kg\cdot m^{ - 3}}$. Jakou hustotu by musela mít druhá koule, aby rozdíl v časech dopadu obou koulí byl větší než $ΔT = 0,3\, \jd{s}$?
- S jakou přesností ověřuje původní Eötvösovo měření rovnosti poměru gravitační a setrvačné hmotnosti pro neutrony a protony, pokud ve dřevě tvoří neutrony 50 procent hmotnosti, zatímco v platině 60 procent hmotnosti? Zanedbejte hmotnost elektronů a vazebné energie.
- Ověřte užívaný předpoklad o tom, že v Budapešti je $g_{s}$ v porovnání s $g$ zanedbatelné.
Zadali autoři seriálu Jakub Benda a Pavel Motloch.