1. Série 24. Ročníku

 

• mezi vodami

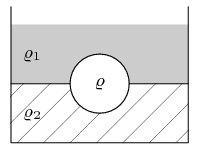
Na rozhraní dvou nemísitelných kapalin se vznáší pevná homogenní koule o hustotě ρ (viz obrázek). Horní kapalina má hustotu $ρ_{1}$, dolní $ρ_{2}$, přičemž víte, že $ρ_{1} < ρ < ρ_{2}$. Jaká část objemu koule se nachází v horní a jaká v dolní kapalině?

• sesterská planeta

V posledních několika letech již byla objevena spousta planet ležících mimo Sluneční soustavu. Daleko zajímavější by bylo ovšem objevovat planety, které jsou podobné Zemi. Předpokládejte, že chcete objevit podobnou Zemi (terestrická planeta s podobným poloměrem jako Země), která obíhá svou hvězdu podobnou Slunci (stejná spektrální třída – podobná hmotnost, podobný poloměr) jednou za pozemský rok. Předpokládejte, že tato soustava je vzdálená od našeho Slunce zhruba 10 pc. Určete podmínky, za kterých by šlo pozorovat planetu přímo z poklesu jasnosti hvězdy a odhadněte dobu, na kterou tato situace nastane. Jak se zkomplikuje hledání takové hvězdy, když soustava bude mít víc planet?

Jakub má u babičky káču, na jejíž horní ploše je nakreslená spirála. Káču roztočíme a díváme se na ní shora. Jaké obrazce pozorujeme a proč?

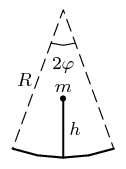
Nehmotná tyč délky $h$ je ve středu připevněna na nehmotný oblouk o vrcholovém úhlu 2φ a poloměru $R$. Na konci tyče je závaží $m$. Pohyb probíhá pouze v rovině. Určete - za jakých podmínek může být soustava stabilní, - frekvenci kmitů takového houpacího koně.

Mára si koupil bublifuk a jal se na balkoně vyfukovat bubliny, venku byl stálý atmosférický tlak $p_{0}$. Když se mu jedna obzvláště povedla (měla poloměr $r$ a hmotnost mýdlové vody byla $m)$, zamyslel se a vypočítal její celkovou tepelnou kapacitu. Učiňte totéž.

Dva světaznalí cestovatelé, jeden tlustý a jeden hubený, se cestou v letadle dohadují o tom, kdo z nich by déle přežil v extrémních podmínkách daleko od civilizace. Rozsoudíte je, kdo vydrží déle ve velkém horku (50 °C), v mrazu (-1 °C), po ztroskotání lodi uprostřed Středozemního moře, v hurikánu nebo při silném sněžení? A jak by to mohlo dopadnout, kdyby je zastihlo mohutné zemětřesení v centru velkoměsta? Kromě jejich tělesné stavby mezi nimi nejsou žádné rozdíly, oba jsou stejně oblečení a nic dalšího s sebou nemají (žádné jídlo, vodu, sirky ani jiné vybavení). Snažte se být nápadití a všímejte si i maličkostí.

Všichni dobře víme, že ve vakuu doletí všechny předměty vržené stejnou rychlostí a pod stejným úhlem stejně daleko. Co se ale stane, když je takto hážeme za normálního tlaku? Změřte, jak závisí dolet tělesa konkrétního tvaru na jeho hmotnosti. Jak tato závislost vypadá teoreticky? Můžete ji spočítat, nebo nasimulovat na počítači např. v Excelu.

a) Uvědomte si, že $n$-té odmocniny z komplexní jednotky leží na $n$-úhelníku, a dořešte Bombelliho rovnici $x^{3}-15x-4 = 0$. Nápovědu naleznete v textu seriálu.

b) Vyjádřete goniometrické součtové vzorce pomocí komplexních exponenciál.

c) Ukažte oprávněnost zanedbání vyšších mocnin v odvození Bernoulliho limity, tj. že do závorky můžeme přidat člen $o(1/N)$.

d) Použijte značení s malým $o$, abyste vyřešili úlohu, s jakou frekvencí kmitají body hmotnosti $m$ po ose $x$ v Yukawově potenciálu $\frac{k}{x}e^{x/λ}$ kolem rovnovážné polohy.

e) Dokažte, že Čebyševovy polynomy $\cos(n \arccos x)$ jsou skutečně polynomy.

Návod: Uvažujte komplexní jednotku $z$, která má reálnou část $x$. Pak se vyšetřovaný výraz rovná reálné části $z^n$, což musí být polynom, protože odmocniny a imaginární jednotky drží pospolu.