2. Série 25. Ročníku
Termín uploadu: -
(2 body)1. chromohrátky
Jak by vypadala duha, kdyby místo deště ze sladké vody pršel třeba olej, kyselina sírová nebo sklo?
Dominika viděla duhu.
(2 body)2. zelený skřítek
Co uvidí člověk, když si stoupne na konec duhy?
Dominika se zadívala do duhy.
(4 body)3. výtah pro lodě
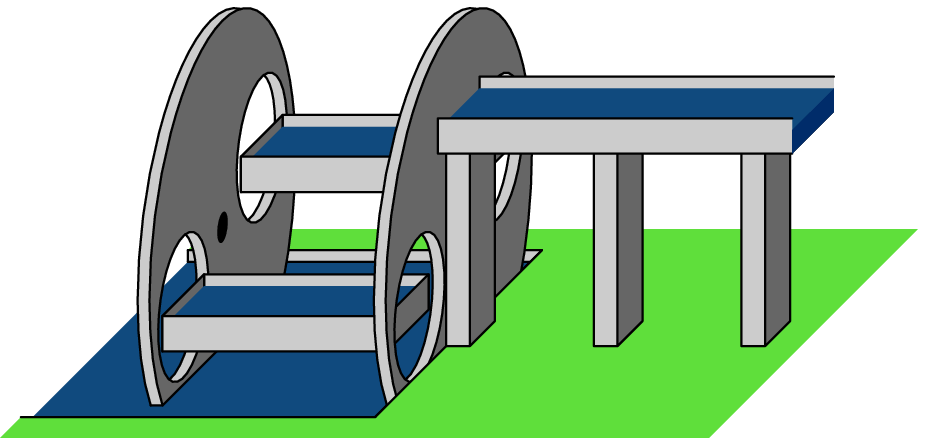
V jednom skotském městečku si postavili výtah pro lodě. Jde o dvě velké vany plné vody na koncích dlouhého ramena, které je uprostřed zavěšeno. Do vany najede loď a pomocí motoru se začne s ramenem otáčet. Jaký výkon musí mít motor, aby takto loď zvedl?
Petr.
(4 body)4. kulička ve vlaku

Mějme svislou desku a ve vzdálenosti $d$ od ní kuličku o hmotnosti $m$ na závěsu délky $l$. V určitém okamžiku se celá soustava začne pohybovat se zrychlením $a$ ve směru kolmém na desku. Určete podmínku pro velikost zrychlení, aby se kulička desky dotkla, a za jak dlouho k tomu dojde, víte-li, že vzdálenost $d$ není větší než jedna pětina $l$.
Petr.
(4 body)5. Mikulášovy kučery
Lidský vlas má u některých lidí tendenci zaujmout zakroucený tvar. Uvažujme vlas, který má v klidovém stavu dané parametry podobně jako stočená pružinka (poloměr, sklon, materiálové konstanty). Spočítejte, jak se vlas prodlouží, když ho nejprve položíme vodorovně na stůl a potom ho pověsíme svisle dolů. Uvažujte hodně stočený vlas, tj. s malým sklonem.
Jakub studoval vlasy kamaráda.
(5 bodů)P. výtahová
Je možné, že se při pádu výtahu člověk před jistou smrtí zachrání dobře časovaným výskokem? Zjistěte, při jaké největší rychlosti pádu by to bylo možné (rychlost výtahu těšně před dopadem, při které již cestující zahynou si vyhledejte nebo odhadněte).
Terka nechtěla zemřít.
(8 bodů)E. čočkování
V obálce jste spolu se zadáním dostali i dvě čočky. Vaším úkolem je změřit jejich parametry - druh a ohniskovou vzdálenost.
Poznámka: Pokud nejste stávající řešitelé FYKOSu, ale máte zájem se jimi stát, pak neváhejte a objednejte si čočky až domů. A to s dostatečným předstihem, aby vám stihly dojít včas. Objednávejte na emailu <tt>cocky@fykos.cz</tt>.
Karel vykradl katedru didaktiky fyziky.
(6 bodů)S. vzdálenosti a černé těleso
- Absolutně černé těleso z definice pohltí všechno světlo, co na něj dopadne, ve všech vlnových délkách. Zároveň je to ideální zářič s charakteristickým spektrem. Můžeme si ho představit třeba jako temné okno domu. Slunce však na první pohled enegrii pouze vydává. Jak je tedy možné, že jeho zážení lze v prvním přiblížení aproximovat absolutně černým tělesem?
- V textu jsme vyjádřili Planckovu funkci jako funkci vlnové délky a teploty. Zkuste ji vyjádřit v závislosti na teplotě a frekvenci. Dokažte, že pro velké vlnové délky a vysoké teploty Planckova funkce přechází v Raighleyův-Jeansův zákon $B_{λ}(T)=2ckT/λ^{4}$ a naopak ve Wienův zákon $B_{λ}=2hc^{2}/λ^{5}$ $\exp(-hc/λkT)$ pro nízké teploty a malé vlnové délky.
- Kruh, který napozoroval Hubbleův vesmírný dalekohled v supernově SN1987A, má podél hlavní poloosy úhlový průměr 1,66''. Má jít o cirkulární objekt, který je díky natočení vůči nám pozorován jako elipsa (viz zde). Světlo ze vzdálenější části elipsy doletělo k Zemi o 340 dnů později, než z bližšího konce. Proměřte fotografii a určete úhel natočení vůči pozorovateli a zkuste spočítat poloměr kruhu. S pomocí trigonometrie určete vzdálenost objektu.
- Pro určení červeného posuvu se zpravidla používají spektrální čáry vodíku. Odhadněte, do jaké hodnoty červeného pousuvu $z$ se pomocí spekter můžeme dostat. Zkuste zjistit (nebo navrhnout), jak se měří $z$ u vzdálenějších objektů.
Janap.