2. Série 30. Ročníku
Termín uploadu: -
(3 body)1. rande na pláži
Představte si, že vezmete svou přítelkyni/svého přítele na večerní rande na pláž a sledujete západ slunce nad vzdálenou hladinou moře. Protože chcete prodloužit romantickou chvilku, vezmete si s sebou vysokozdvižný vozík, který se, jakmile slunce začne zapadat za obzor, začne rovnoměrným pohybem zvedat vzhůru, abyste stále viděli slunce dotýkající se horizontu. Jakou rychlostí se musí vozík pohybovat?
Dominika vzpomínala na Itálii.
(3 body)2. hypervysokoteplotní supravodivost
Velké části látek, obvykle kovům, roste s vyšší teplotou odpor. Jsou ovšem látky, jako například grafit či polovodiče, kterým odpor s rostoucí teplotou klesá. Také jste již pravděpodobně slyšeli o supravodivosti, což je jev, který obvykle nastává za velmi nízkých teplot a jedná se o stav, ve kterém látka nevykazuje žádný elektrický odpor a dokonale vede elektrický proud. V současné době jsou nejvyšší teploty, ze kterých byla supravodivost pozorována, hluboko pod pokojovou teplotou. Co kdybychom ale uvažovali, že se odpor mění dle vzorečku $R=R_{0}(1+αΔt)$, kde $R_{0}$ je odpor vodiče pro $20\; \mathrm{°C}$, $α$ je teplotní součinitel elektrického odporu a $Δt$ teplotní rozdíl vůči původní teplotě $20\; \mathrm{°C}$? Tak při hodnotách součinitelů pro grafit $α_\mathrm{C}=-0,\! 5 \cdot 10^{-3}\; \mathrm{K^{-1}}$ a křemík $α_\mathrm{Si}=-75 \cdot 10^{-3}\; \mathrm{K^{-1}}$ dostáváme nulový odpor pro vysoké teploty. Pro jaké? A jak to, že to ve skutečnosti nefunguje a jak uhlík, tak křemík nejsou za vysokých teplot supravodivé?
Karel se inspiroval nekonstantními konstantami.
(6 bodů)3. looping
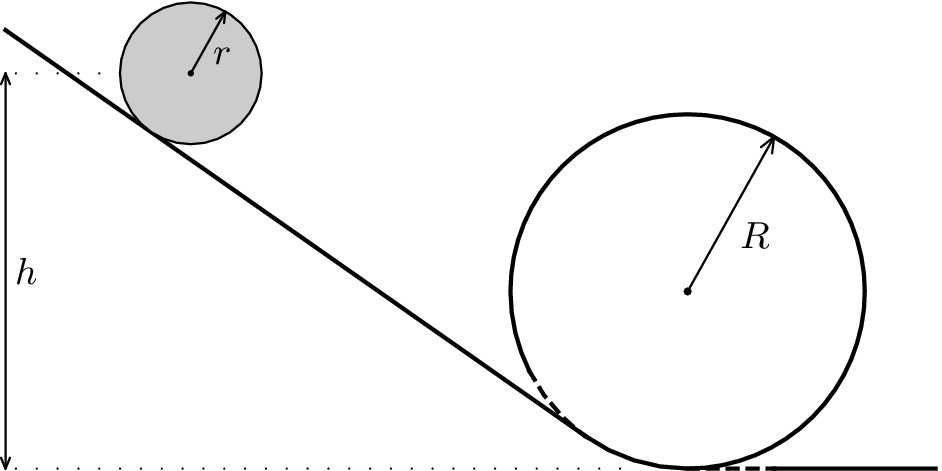
Mějme nakloněnou rovinu pod úhlem $α$, na kterou hladce navazuje kruhová smyčka o poloměru $R$. Do jaké minimální výšky $h$ musíme na nakloněnou rovinu položit kouli o poloměru $r$ (srovnatelném s $R$), aby smyčkou projela tak, že s ní bude po celou dobu v kontaktu? Předpokládejte, že koule neprokluzuje.
Kuba přemýšlel nad klasickou úlohou.
(6 bodů)4. kulička
Představte si pohyb homogenní kuličky, který nejprve začíná pouze posunem (bez jakéhokoliv pohybu valením) a postupně přejde do naopak naprostého valení (bez prokluzování). Za jaký čas toto nastane? Kulička může mít různý poloměr, hmotnost, počáteční rychlost a třecí koeficient.
Lada dělala kotrmelce u zamyslela se u toho.
(7 bodů)5. várnice potřetí
Uvažujte klasickou várnici s kohoutkem dole a se vzduchotěsným víkem nahoře. Kolik čaje je možné si nalít, než budeme muset otevřít ventil, který vyrovná tlak vzduchu nad čajem s okolním tlakem?
Lukáše na soustředění trápilo, kolik čaje má být ve várnici.
(9 bodů)P. efektivní (ná)stroj
Palné zbraně jsou vlastně takovými tepelnými stroji. Spočítejte jaká je účinnost nějaké pušky nebo pistole. (Jde o využití energie střeliva pro pohyb kulky.)
Michal původy svých nápadů raději nesděluje.
(12 bodů)E. jedno plnotučné, prosím
Tučnější mléko by mělo být „bělejší“ – více světla rozptýlí a méně propustí skrz. Proveďte měření tučnosti mléka na základě rozptylu světla, přičemž jako barevnou škálu použijte přiložený papírek (pokud jste neřešili první sérii a chcete obdržet papírek, napište nám na fykos@fykos.cz). Rozdíly nejlépe vyniknou, pokud do různých druhů mléka budete přidávat barvivo tak, aby jej v mléku byla stejná (malá) koncentrace. Jako barvivo můžete použít černou tuš. Samozřejmě je možno použít jakékoliv jiné barvivo, ale pak si budete muset vyrobit vlastní barevnou škálu, kterou prosím přiložte k řešení. Zrealizujte měření pro různé druhy mléka a směsi mléka a vody. Diskutujte spolehlivost určení obsahu tuku.
Mára byl bledý jako stěna.
(10 bodů)S. odhadnutelná
- Zkuste vlastními slovy popsat, k čemu slouží intervalový odhad střední hodnoty v normálním rozdělení a uveďte jeho fyzikální interpretaci (postačí vlastními slovy popsat následující: fyzikální interpretace odhadu střední hodnoty, rozdíl mezi (bodovým) odhadem a intervalovým odhadem, nejdůležitější vlastnost intervalového odhadu, metoda zkráceného zápisu intervalového odhadu, nejistota měření). Není potřeba uvádět přesná matematická odvození, stačí požadované pojmy a vlastnosti stručně popsat.
- V přiloženém datovém souboru mereni1.csv najdete naměřené hodnoty určité fyzikální veličiny (uvažujte nejistotu typu B $s_\mathrm{B} = 0,\! 1$ ). Zkonstruujte z těchto dat bodový i intervalový odhad měřené fyzikální veličiny a krátce interpretujte jejich význam.
- Předpokládejme, že měříme určitou fyzikální veličinu a víme, že vlivem použité metody měření budou mít naměřená data rozptyl rovný konstantě $c$ (nejistotu typu B neuvažujte). Kolik musíme přibližně provést měření, abychom dosáhli nejistoty měření menší než $s$?
- V přiloženém datovém souboru mereni2.csv najdete data měření stejné fyzikální veličiny dvěma různými způsoby (nejistotu typu B neuvažujte). U které metody byla použitá měřící aparatura přesnější? Který způsob měření dal přesnější výsledek měření? U obou otázek své závěry i stručně zdůvodněte.
Bonus: Zkuste odvodit, že v normálním rozdělení je výběrový rozptyl nestranným odhadem skutečného rozptylu (tj. střední hodnota výběrového rozptylu je rovna skutečnému rozptylu).
Pro řešení tohoto úkolu můžete použít libovolné zdroje (pokud je budete řádně citovat). Pro práci s daty použijte výpočetní prostředí R. Pro vyřešení těchto úkolů postačí drobně upravit přiložený skript, ve kterém je pomocí komentářů v kódu vysvětlena potřebná syntaxe jazyka R.
Michal si dal v zadání pozor na hrubé chyby.