6. Série 12. Ročníku
Termín uploadu: -
1. plyn v láhvi
Uzavřená nádoba obsahující ideální plyn se pohybuje rychlostí $v$. Nádoba se náhle zastaví a veškerá kinetická energie plynu se změní v teplo. Zanedbejte teplo předané stěnám a spočtěte, o kolik se zvětší druhá mocnina střední kvadratické rychlosti molekul plynu, je-li plyn
- jednoatomový
- dvouatomový.
Zdůvodněte rozdílné výsledky v jednotlivých případech.
2. dipól v magnetickém poli
Mějme elektrický dipól (představte si ho jako dvě částice se stejnými hmotnostmi $m$ a náboji $+q$ a $-q$ upevněné na koncích nehmotné tyčky délky $l$). Otáčí se v horizontální (vodorovné) rovině okolo vertikální (svislé) osy procházející středem dipólu. Popište pohyb dipólu poté, co zapneme konstantní vertikální magnetické pole $B$.
3. oscilační obvody
Rezonanční obvod se skládá z neideální cívky s indukčností $L=1\,\jd{ H}$ a vnitřním odporem $R=1\,\jd {Ω}$ a neideálního kondenzátoru s kapacitou $C=1\,\jd{µF}$ o neznámém svodovém odporu $R_{x}$. Jaká je velikost $R_{x}$, pokud víme, že se 1/3 původní energie rezonančního obvodu ztrácí v podobě tepla na odporu cívky?
4. míček v kondenzátoru
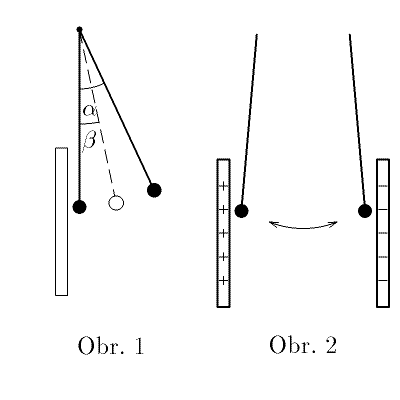
Malá kovová kulička o hmotnosti $m=3,0\,\jd{g}$ je zavěšena na tenkém hedvábném vlákně délky $l=30\;\mathrm{cm}$ tak, aby se dotýkala svislé kovové desky. Kuličku vychýlíme o úhel $α$ a uvolníme. Po odrazu od desky se kulička vychýlí o úhel $β<α$ (obr. 1).
Při druhém pokusu umístíme do vzdálenosti $d=5,0\;\mathrm{cm}$ od první desky druhou stejně velkou. Závěs kuličky prodloužíme, aby byl mnohem delší než vzdálenost desek. Připojíme-li desky ke zdroji vysokého napětí $U=2,00\cdot 10^{4}$ V a závěs vychýlíme, kulička se rozkmitá a naráží střídavě na levou a pravou desku (obr. 2). Perioda nárazů se brzy ustálí na hodnotě $T=0,45\;\mathrm{s}$.
Jak se mění při druhém pokusu rychlost kuličky mezi dvěma nárazy na desky? Jaký náboj nese kulička během letu mezi deskami?
P. gravitace
Už od pradávna se lidé zabývali pozorováním oblohy a později pohybem planet okolo Slunce. Jak se to historicky odehrálo, asi všichni znáte. Tycho de Brahe sledoval mnoho let pohyby planet a zhotovil rozsáhlé tabulky. Z nich vyšel Kepler a objevil své zákony. Těch využil Newton, lépe pochopil podstatu těchto zákonů a dospěl ke krásnému vztahu:
$$F_{G} = G\frac{ mM}{r^{2}}\,.$$
Takto popisujeme pouze pohyb planet okolo Slunce. Můžeme říci, co vyvolává tuto sílu? Tímto se zabýval i Newton a nakonec se uspokojil poznáním toho, co se odehrává, bez znalosti mechanismu. Dodnes jej nikdo neobjevil. Bylo navrženo více mechanismů gravitace. Jeden ze zajímavých je tento:
Představte si, že v prostoru je velké množství částic, které se pohybují velkou rychlostí ve všech směrech a jsou málo absorbované při průchodu hmotou. Když jsou pohlcené Zemí, předávají jí hybnost. Když je těch, které jdou jedním směrem, stejně jako těch z opačného směru, jsou hybnosti vyvážené. Když se k Zemi přiblíží Slunce, jsou částice přicházející na Zemi přes Slunce částečně absorbovány a ve směru od Slunce jich přichází méně než z opačné strany. Země proto získá hybnost směřující k Slunci.
Na vás je, abyste ověřili, jestli je taková gravitační síla nepřímo úměrná čtverci vzdáleností (uvažujte dvě koule, kde jedna je mnohem menší než ta druhá – stačí přibližně). Jak asi tušíte, tento mechanismus gravitace není správný. Zkuste přijít na to, kde selhává.
Návod: Najděte chybné důsledky.
E. atmosférický tlak
Změřte atmosférický tlak v místě vašeho bydliště a to touto metodou: Ponořujte do nádoby s vodou prázdnou skleničku dnem vzhůru a z toho, jak vysoko se dostane voda ve skleničce spočtěte atmosférický tlak. Znáte hustotu vody $ρ$ a tíhové zrychlení $g$. Nezapomeňte uvést místo a čas měření.
S. optická vlákna
- Jak velká je vstupní numerická apertura u vlákna s gradientním indexem lomu $n=1,452$ a relativní změnou indexu lomu $Δ=0,01?$
- Jak dlouhý signál dostaneme na výstupu z optického vlákna s parametry z části a) o délce $100\,\jd {km}$, jestliže dáme na vstup signál dlouhý
$1\,\jd {µs}$? K výpočtům použijte nastíněného geometrického modelu.
- Jakou maximální přenosovou kapacitu (v bytech/s) můžeme na tomto vlákně provozovat? Předpokládejte, že přenesení jednoho bitu znamená přenést jeden impuls.