6. Série 20. Ročníku
Termín uploadu: -
1. tři válce děda Vševěda
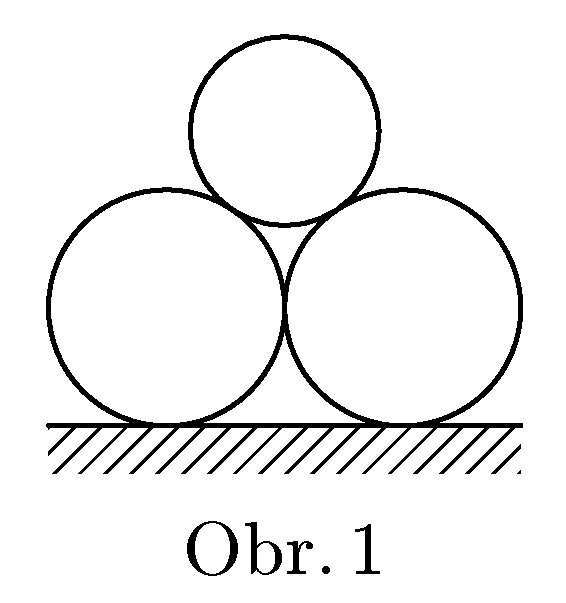
Zjistěte, za jakých podmínek bude soustava tří válců na obrázku 1 v rovnováze. Hustota materiálu válců je $ρ$, spodní válce mají poloměr $R$, horní válec má poloměr $r$. Součinitel tření je mezi všemi povrchy stejný.
Zadal Honza Prachař, aby prověřil vaše znalosti ze statiky soustavy tuhých těles.
2. podivná atmosféra
Okolo planety o poloměru $R$ se nachází atmosféra, jejíž index lomu se mění s výškou podle vztahu $n=n_{0}-αh$. Zjistěte, v jaké výšce $h$ nad povrchem planety se světelný paprsek vyslaný tečně k povrchu bude pohybovat po kružnici okolo planety.
Nepoužitá úloha z archivu.
3. čtverák čtverec
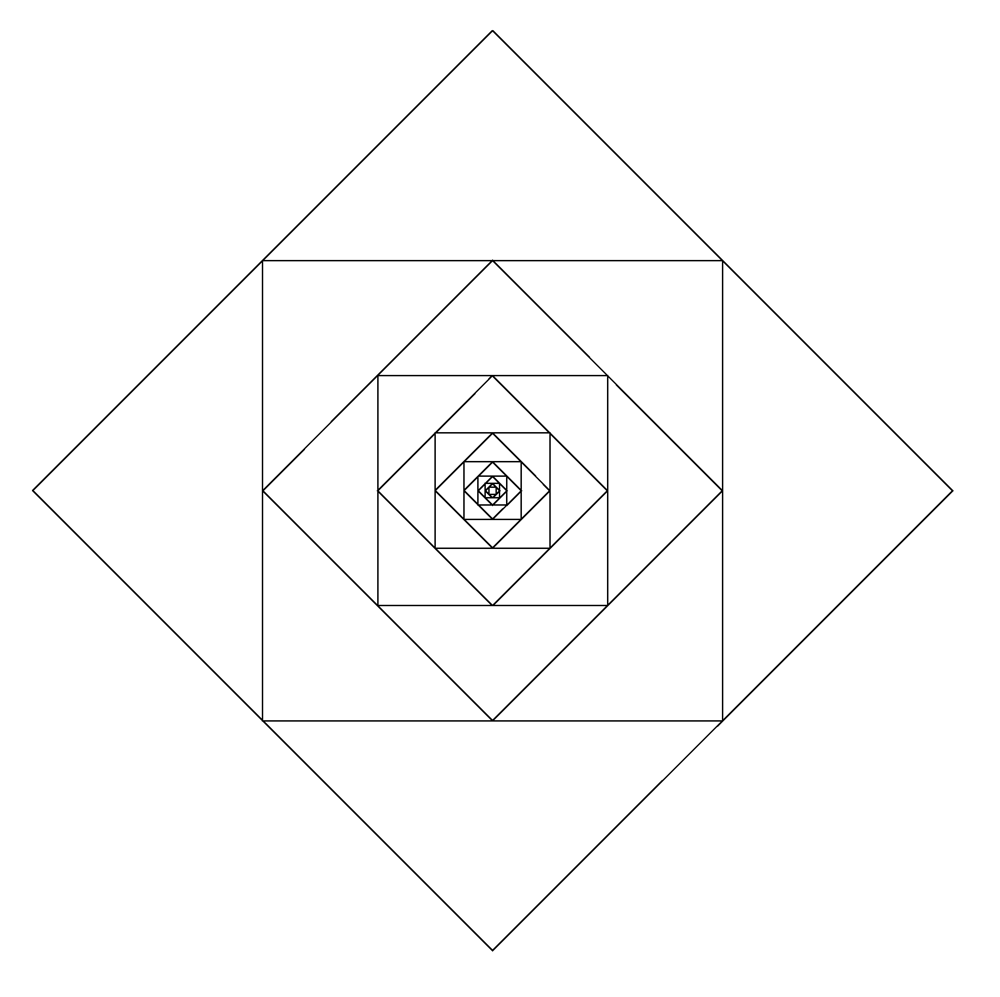
Obvod na obrázku vznikne spojením nekonečně mnoha drátěných čtverců, přičemž každý následující je √2 -krát menší. Drát, ze kterého je obvod vyroben, o délce rovné straně největšího čtverce má odpor $R$. Určete odpor obvodu mezi krajními body vlevo a vpravo.
Úlohu vymyslel Marek Pechal.
4. zákrytová dvojhvězda
Magnituda jisté zákrytové dvojhvězdy se mění se čtyřdenní periodou v této posloupnosti:
vedlejší minimum $m = 3,5$ ,
maximum $m = 3,3$ ,
hlavní minimum $m = 4,2$ ,
maximum $m = 3,3$ .
Větší složka této dvojhvězdy má také vyšší teplotu než její průvodce. Za předpokladu, že Země leží v oběžné rovině dvojhvězdy, vypočítejte magnitudy jednotlivých složek a poměr jejich délkových rozměrů. Převodní vztah mezi magnitudou $m$ hvězdy a osvětlením $E$, které způsobuje, je
$m=-2,5\log(E⁄E_{0})$,
kde $E_{0}$ je pevně definovaná hodnota.
Nepoužitá úloha z archivu.
P. jak vypadají ufoni?
Zamyslete se nad tím, jestli by nějaké zvíře mohlo teoreticky komunikovat pomocí elektromagnetických vln rádiových frekvencí $(10\, \jd{Hz}\, –\, 100\, \jd{MHz}). Zkuste navrhnout, jak by vypadaly biologické ekvivalenty potřebných elektrických součástek.
Zadal Michael Komm doufaje, že přijdete na něco zajímavého.
E. slintací úložka
Změřte, jaký maximální podtlak (i přetlak) je člověk schopen vyvinout sáním (nafukováním) ústy.
O ruce vás chtěl připravit Michael Komm.
S. lineární harmonický oscilátor ve vnějším poli
Viz přiložený soubor.
Zadal autor seriálu Jarda Trnka.