1. Série 28. Ročníku
Termín uploadu: -
(2 body)1. spotřeba antihmoty
Jakou hmotnost antihmoty bychom potřebovali ročně, abychom pokryli spotřebu elektrické energie České republiky? Normální hmoty máme dost a uvažujme, že by se nám energii podařilo na elektrickou převádět beze ztrát.
Karel se díval na Anděly a Démony od Dana Browna.
(2 body)2. proudivé proudnice
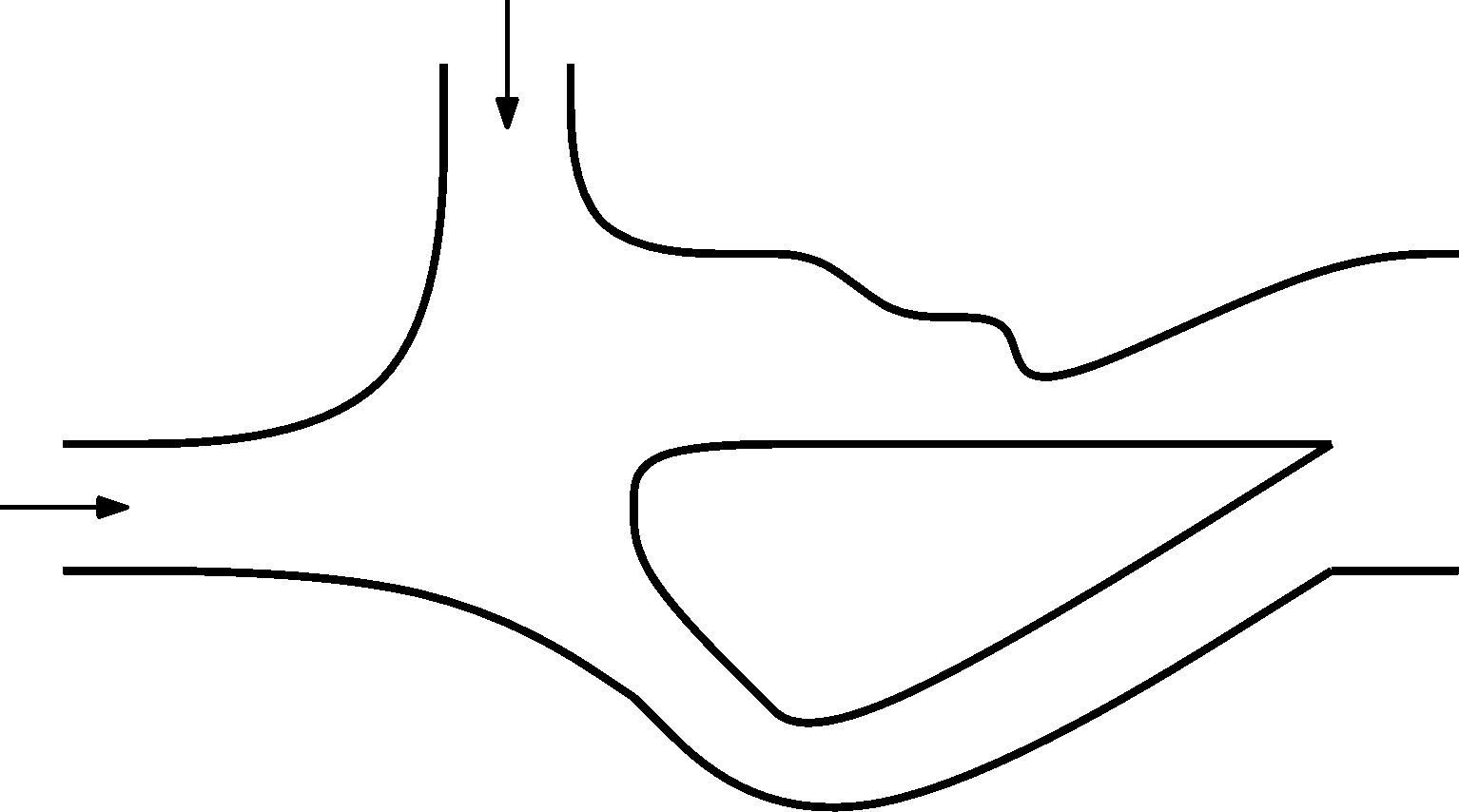
Nakreslete do obrázku proudnice. Do obou otvorů s šipkou vtéká stejné množství vody, všechna voda pak vytéká jediným, třetím otvorem. Proudění je ustálené a probíhá dostatečně pomalu, abychom ho mohli považovat za nevířivé. Při kreslení dbejte na pravidla, jimiž se tvar proudnic řídí a tato pravidla napište jako komentář k obrázku. Neočekáváme, že bude problém spočítán.
Poznámka: Kreslete do většího obrázku dostupného z webu.
kolar
(3 body)3. zrychlujeme
Vysvětlete, proč a jak se odehrají následující situace:
- V cisterně tvaru kvádru s vodou plove na hladině míček. Popište pohyb míčku, začne-li se cisterna rozjíždět s konstantním zrychlením dostatečně malým, aby voda nepřetekla přes okraj.
- V cisterně tvaru kvádru naplněné vodou se vznáší balonek naplněný vodou. Popište pohyb balonku, začne-li se cisterna rozjíždět s konstantním zrychlením dostatečně malým, aby voda nepřetekla přes okraj.
- V uzavřeném autobusu se vznáší u stropu balonek. Popište jeho pohyb, začne-li se autobus rozjíždět s konstantním zrychlením.
Dominika a Pikoš na zkoušce z fyziky.
(4 body)4. zkáza Titaniku
Náry si vždy přál mít loďku, a tak si jednoho krásného dne pořídil jednu ve tvaru kvádru bez horní podstavy (jako vana) s vnějšími rozměry $a$, $b$, $c$ a tloušťkou stěny $d$, která byla vyrobena z voňavého dřeva o hustotě $ρ$ (větší než hustota vody). Druhého krásného dne loďku spustil na vodu, ale zjistil, že má na dně dírku, kterou voda přitéká s průtokem $Q_{1}$. To bylo nemilé, a protože je mužem činu, začal počítat, za jak dlouho se mu do loďky začne valit voda vrchem. Stejnou otázku klade i tato úloha. Zvažte i situaci, kdy by Náry o hmotnosti $m$ v loďce seděl a mezi výpočty zoufale vyléval vodu svou botou s průtokem $Q_{2}$. Loďka je celou dobu vodorovně.
Kiki zaslechla o problému s tím, že skoro všechny úlohy vymýšlí Karel.
(5 bodů)5. tisícročná včela
Spočítejte, jaký výkon potřebuje včela, aby se udržela ve vzduchu, a odhadněte, jak dlouho se vydrží najedená včela vznášet v konstantní výšce.
Michalovi vyplynulo z diskuze o kvadrokoptérách.
(5 bodů)P. Měsíc z Marsu
Může být někdy vidět Měsíc z Marsu pouhým okem? Svou odpověď podpořte náležitými výpočty.
Kuba chtěl být stručný.
(8 bodů)E. nabitá brambora
Změřte zátěžovou charakteristiku brambory jako zdroje elektrického napětí se zapojenými elektrodami z různých kovů.
Karel přemýšlel nad jednoduchými pokusy.
(6 bodů)S. nejistá
- Sepište si rovnice pro vrh v homogenním gravitačním poli (nemusíte je znovu řešit, ale musíte je umět správně použít). Navrhněte přístroj, který bude vrhat předmět dle vašeho uvážení a určete pod jakým úhlem a jakou rychlostí tak činí. Můžete například vrhat pomocí pružiny, změřit její tuhost, hmotnost předmětu a vypočítat kinetickou energii a tudíž i rychlost předmětu. V jakých rozmezích jste si s rychlostí a úhlem jistí? Dosaďte tyto rozsahy do rovnic a ukažte v jakých rozmezích v důsledku toho můžete očekávat vzdálenost dopadu od vašeho předmětu. Vrhněte svůj předmět daný přístrojem alespoň pětkrát a změřte vzdálenost dopadu – v jakých rozmezích jste si jisti danou vzdáleností? Ukažte, zda se vešly vaše výsledky do toho, co jste předpověděli. (Za odkaz na video s vrhem bonusový bod!)
- Uvažte kyvadlo s výchylkou $x$, které se efektivně kývá harmonicky, ale frekvence jeho kyvů závisí na maximální výchylce $x_{0}$
$$x(t) = x_0 \cos\left[\omega(x_0) t\right]\,, \quad \omega(x_0) = 2\pi \left(1 - \frac{x_0^2}{l_0^2}\right)\,,$$
kde $l_{0}je$ nějaká délková škála. Myslíme si, že pouštíme kyvadlo z $x_{0}=l_{0}⁄2$, ale ve skutečnosti jej vypouštíme z $x_{0}=l_{0}(1+ε)⁄2$. O kolik se liší argument kosinu od 2π po jedné námi předpokládané periodě? Po kolika periodách bude kyvadlo vychýlené na druhou stranu, než bychom předpokládali? Tip Argument kosinu se bude v tu chvíli od předpokládaného lišit o víc než π ⁄ 2.
- Vezměte do ruky propisku a postavte jí na stůl na špičku. Proč spadne? A co rozhoduje o tom, že spadne spíš doprava, než doleva? Proč nedokážete předpovědět výsledek hodu kostkou, i když zákony fyziky by jej měly plně předurčit? Když hrajete kulečník, je neschopnost dokončit hru pouze v jednom šťouchu pouze v tom, že to nedokážete propočítat? Sepište svoje odpovědi a zkuste vyjmenovat fyzikální jevy ze života, které jsou v principu předpověditelné, ale ani dobrá znalost situace vám v předpovědi moc nepomůže.