4. Série 30. Ročníku

Pohádkové postavy to nemají lehké, chtějí-li zjistit, kdy se objevují na scéně. Dnešní technika jim to ale usnadňuje. Třeba princezna Pointa z pohádky o délce šest kapitol. Všechny kapitoly jsou stejně dlouhé, a tak každá na Karlově displeji měří $1200$ pixelů na výšku (samotný displej ale zobrazí jen výšku $900\; \mathrm{px}$). Při čtení Karel souvisle scrolluje a navíc čte pořád stejně rychle. Po třech minutách od začátku čtení Pointa minula první konec posuvníku ve scrollbaru a po sedmi minutách i druhý. V kolikáté kapitole se objeví Pointa?

Poznámka: Poměr výšky posuvníku vůči výšce displeje je stejný jako poměr výšky displeje vůči výšce celého textu pohádky.

Je známou skutečností, že aby byla jízda vlakem co nejpohodlnější, pak při rozjíždění a brzdění je potřeba, aby se zrychlení měnilo co nejméně. Proto je dobré, když se vlak rozjíždí s malou konstantní změnou zrychlení. Změna zrychlení se nazývá ryv. Určete, jak se v čase mění stabilní poloha kyvadla (úhel odklonění od svislice $φ$). Délku kyvadla označme $l$, vlak se rozjíždí na rovině, ryv označme $k$ ($k=Δa/Δt$, kde $a$ je zrychlení) a vlak jede po Zemi s normálním tíhovým zrychlením $g$.

Bonus: Sestavte pohybové rovnice, které numericky vyřešte pro $φ(0)=0$ a $dφ/dt(0)=0$ pro různé hodnoty $k$.

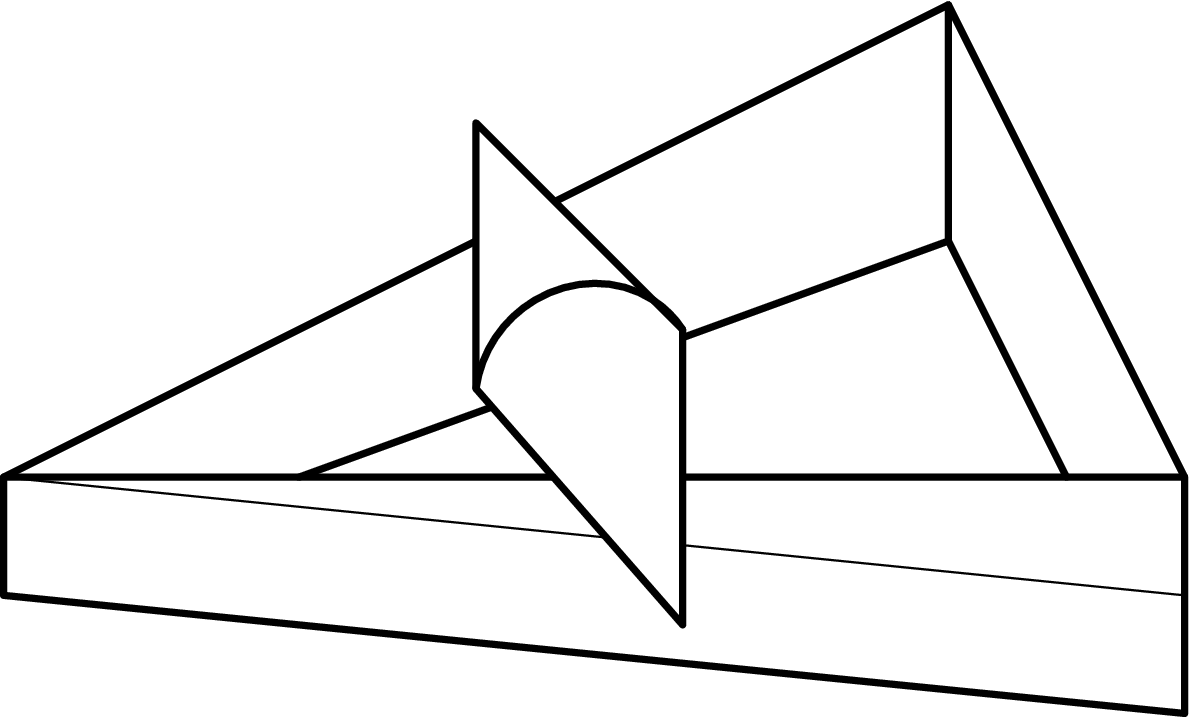
Mějme dřevěnou konstrukci, která má půdorys rovnoramenného trojúhelníku a výška jejích dvou ramen roste směrem k základně s úhlem $α=2°$. Do vrcholu naproti základně $c=35\;\mathrm{cm}$, u nějž má trojúhelník úhel $β=70°$, umístíme dvojkužel s vrcholovým úhlem $φ=40°$ a výškou $2h=40\;\mathrm{cm}$. Kužel se samovolně začne valit „do kopce“, tedy ve směru růstu hran trojúhelníku.

• Vysvětlete, proč se dvojkužel může kutálet do kopce.
• Jak závisí poloha těžiště kuželu na uražené vzdálenosti?
• Jaká je rychlost kužele těsně před nárazem na základnu?
• Kolik otáček kužel vykoná během své cesty?

Na počátku je kužel umístěn horizontálně na konstrukci tak, že jeho těžiště se nachází přesně nad vrcholem trojúhelníku proti základně.

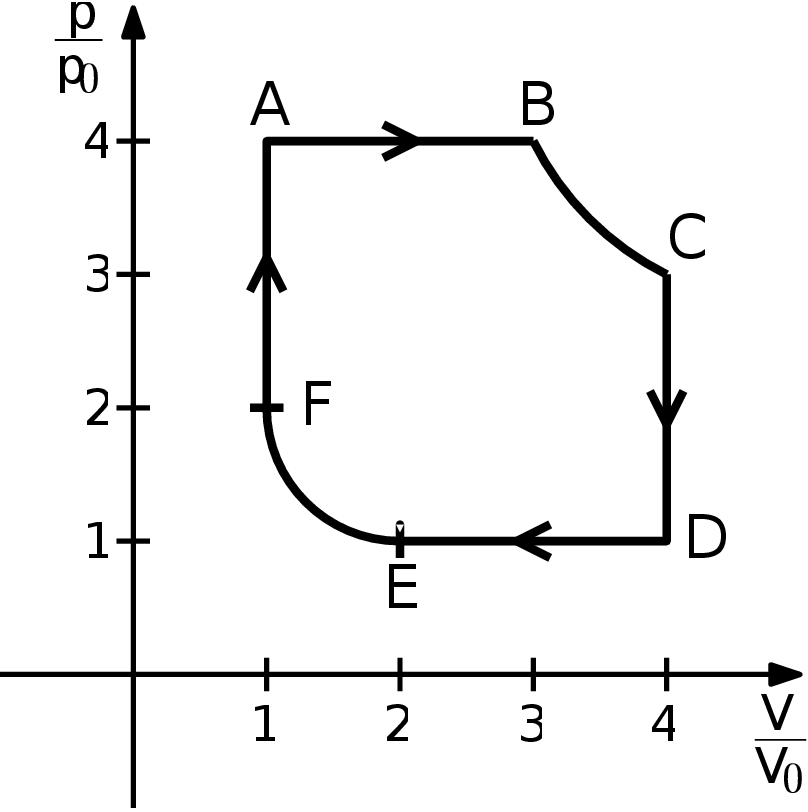
Mějme tepelný stroj naplněný ideálním plynem složeným z dvouatomových molekul. Tento tepelný stroj vykonává kruhový děj $\mathrm{ABCDEFA}$ (viz obrázek), tedy skládá se z šesti dějů

• $\mathrm{A} \longrightarrow \mathrm{B}$ - izobarické zahřátí ze stavu $4p_{0}$ a $V_{0}$ (teplotu v A označme jako $4T_{0}$) do stavu s objemem $3V_{0}$,
• $\mathrm{B} \longrightarrow \mathrm{C}$ - izotermická expanze na objem $4V_{0}$,
• $\mathrm{C} \longrightarrow \mathrm{D}$ - izochorické ochlazení na tlak $p_{0}$,
• $\mathrm{D} \longrightarrow \mathrm{E}$ - izobarické ochlazení na objem $2V_{0}$,
• $\mathrm{E} \longrightarrow \mathrm{F}$ - izotermická komprese na objem $V_{0}$,
• $\mathrm{F} \longrightarrow \mathrm{A}$ - izochorické zahřátí na tlak $4p_{0}$. Určete zbývající stavové veličiny ve stavech $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$, $\mathrm{E}$ a $\mathrm{F}$, maximální a minimální teplotu ideálního plynu v průběhu děje (v násobcích $T_{0}$), teplo přijaté či odevzdané plynem v jednotlivých dějích a účinnost tepelného stroje. Srovnejte tuto účinnost s účinností Carnotova stroje pracujícího se stejnými maximálními a minimálními teplotami. Pro jednoduchost uvažujte, že se nemění látkové množství plynu ve stroji a nedochází v něm k chemickým přeměnám.

Bonus: To samé proveďte pro jednodušší cyklický „čtvercový“ děj, tedy $\mathrm{ABCDA}$, kde plyn začíná ve stavu $p_{0}$, $V_{0}$ a $T_{0}$ a izochoricky se ohřeje na $4p_{0}$, izobaricky se zahřeje a rozepne na $4V_{0}$, izochoricky ochladí na $p_{0}$ a izobaricky se ochladí na $V_{0}$. Srovnejte účinnosti těchto dvou tepelných strojů a diskutujte, který je lepší.

Zažili jste už někdy takovou divnou atmosféru? Do určité výšky je v ní rychlost šíření světla konstantní $v_{0}$ a od určité hranice se rychlost šíření světla začne lineárně zvětšovat podle vztahu $v(Δh)=v_{0}+kΔh$. V jednom místě, právě ve výšce, kde se začala měnit rychlost světla, vyšleme světelné paprsky pod všemi možnými úhly směrem nahoru. Ukažte, že se budou všechny paprsky pohybovat po částech kružnic a určete poloměry těchto kružnic. Také určete vzdálenost od místa vypuštění paprsků, kde se paprsky vrátí do původní výšky.

Známe to všichni, krajíc chleba namazaný medem nebo marmeládou, zakousneme se a najednou je kapka mazadla na ruce a jsme za prasata. Spočítejte, jak závisí pravděpodobnost, že v krajíci bude díra skrz naskrz, v závislosti na jeho tloušťce. Model kynutí těsta necháme na vás. (Třeba rovnoměrně rozmístěné bubliny s exponenciálně rozděleným poloměrem je dobrý model.)

Změřte povrch ptačího (např. slepičího) vejce.

• Zkuste vlastními slovy popsat, k čemu a jak se používá testování hypotéz (postačí vlastními slovy popsat následující: hypotéza a alternativa, chyba 1. a 2. druhu, hladina testu, testová statistika, kritický obor testu, $p$-hodnota testu pro konkrétní naměřená data). Není potřeba uvádět přesná matematická odvození, stačí požadované pojmy a vlastnosti stručně popsat.
• V přiloženém datovém souboru testovani1.csv najdete naměřené hodnoty určité fyzikální veličiny. Pomocí jednovýběrového $t$-testu otestujte, zda je skutečná hodnota měřené fyzikální veličiny rovna $20$. Dále předpokládejme, že je naším cílem ukázat, že hodnota měřené fyzikální veličiny je větší než $20$. Použijte vhodnou jednostrannou modifikaci $t$-testu k tomu, abyste toto tvrzení ověřili (dejte si pozor na správné zvolení hypotézy a alternativy).
• V přiloženém datovém souboru testovani2.csv najdete naměřené hodnoty 2 různých fyzikálních veličin. Představujme si, že se jedná o měření stejné fyzikální charakteristiky ale za různých vnějších podmínek (teplota, tlak atd.). Pomocí dvouvýběrového $z$-testu otestujte hypotézu, že hodnota této fyzikální charakteristiky je pro obě volby vnějších podmínek stejná.
• Použijte stejná data jako v seriálové úloze z první série a pomocí Kolmogorovova-Smirnovova testu určete, který ze 4 vzorků dat pochází z normálního rozdělení a který vzorek pochází z exponenciálního rozdělení.

Bonus: Předpokládejte, že máte k dispozici měření 2 fyzikálních veličin (tedy 2 sady naměřených hodnot), kde jsou všechna měření na sobě nezávislá. Odvoďte upravený dvouvýběrový $z$-test, který by testoval hypotézu, že skutečná hodnota první měřené fyzikální veličiny je dvojnásobek skutečné hodnoty druhé měřené fyzikální veličiny. Pro udělení bodů je nutné a postačuje odvodit podobu testové statistiky a kritického oboru (Nápověda: Použijte vícerozměrnou verzi CLV, kde vhodně zvolíte funkci $f$, a dále postupujte analogicky jako u odvození klasického dvouvýběrového $z$-testu.).

Pro práci s daty použijte výpočetní prostředí R. Pro vyřešení těchto úkolů postačí drobně upravit přiložený skript, ve kterém je pomocí komentářů v kódu vysvětlena potřebná syntaxe jazyka R.

• skript v kódování UTF-8
• skript v kódování CP-1250
• testovani1.csv
• testovani2.csv